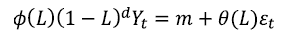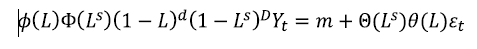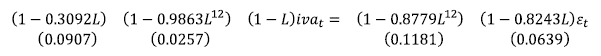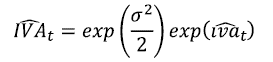Erick Galarza Molina

Universidad de Cuenca. Cuenca, Ecuador erickb.galarza@ucuenca.edu.ec.
Patricio Baculima Cuesta

Universidad de Cuenca. Cuenca, Ecuador patricio.baculimac@ucuenca.edu.ec.
Alfredo Loja Villalta

Universidad de Cuenca. Cuenca, Ecuador alfredoa.loja@ucuenca.edu.ec.
Karla Sigüenza García

Universidad Técnica Particular de Loja. Loja, Ecuador kysiguenza@utpl.edu.ec.
Resumen
En Ecuador, la recaudación tributaria del IVA causado supera el 50 % del total de recaudación tributaria, siendo a su vez los grandes contribuyentes quienes conforman la parte mayoritaria de la recaudación tributaria por sectores, por lo que la modelación y pronóstico de la evolución de la variable impositiva resulta relevante para la planificación presupuestaria estatal. La presente investigación pretende modelar la recaudación tributaria del IVA causado de los grandes contribuyentes en el período 2011-2023 mediante modelos estacionarios lineales, como los procesos ARIMA y SARIMA, utilizando la metodología de Box-Jenkins y los criterios informacionales para la estimación y validación del modelo; además, pronosticar la evolución de la variable tributaria hacia 2024. Una vez identificado el modelo adecuado con un ajuste prácticamente perfecto —siendo este un SARIMA (1,1,1) X (1,0,1)12— el pronóstico para 2024 indica que la recaudación aumentará en un 4,73 % con respecto a 2023 en diciembre, planteándose algunas posibles causantes de este comportamiento. En 2024 se mantiene una especie de ciclo recaudatorio con puntos máximos en el último mes, mientras que en los demás la actividad se ralentiza. Una limitante de esta investigación es la no consideración de efectos GARCH y de variables de control dentro de la estimación, por lo que se recomienda a futuras investigaciones considerar estas pautas.
Palabras clave: tributación, econometría, previsión económica, contribución presupuestaria, política fiscal.
JEL: H25 Impuestos y subvenciones sobre rentas empresariales.
Abstract
In Ecuador, VAT incurred tax collection exceeds 50 % of total tax collection, with large taxpayers make up the majority of tax collection by economic sector, so that modeling and forecasting the evolution of the tax variable is relevant for the formulation of public policies and state budget planning. This research aims to model the VAT incurred tax collection of large taxpayers in the period 2011-2023 through linear stationary models, such as the ARIMA and SARIMA processes, using the Box-Jenkins methodology and informational criteria for the estimation and validation of the model; in addition, to forecast the evolution of this tax variable towards 2024. Once the appropriate model with a practically perfect fit has been identified —this being a SARIMA (1,1,1) X (1,0,1)12—, the forecast for 2024 indicates that collection will increase by 4.73 % with respect to 2023 in December, considering some possible causes of this behavior. In 2024, a sort of collection cycle is maintained with peaks in the last month, while in the others the activity slows down, even in June. A limitation of this research is the non-consideration of GARCH effects and control variables within the estimation, so it is recommended that future research consider these guidelines.
Key words: taxation, econometrics, economic forecasting, budget contributions, fiscal policy
JEL: H25 Taxes and subsidies on business income.
Resumo
No Equador, a cobrança fiscal do IVA suportado excede 50 % da cobrança total de impostos, sendo os grandes contribuintes responsáveis pela maior parte da cobrança de impostos por sector, pelo que a modelação e previsão da evolução da variável fiscal é relevante para o planeamento do orçamento do Estado. Esta investigação tem como objetivo modelar a cobrança fiscal do IVA suportado pelos grandes contribuintes no período 2011-2023 através de modelos lineares estacionários, como os processos ARIMA e SARIMA, utilizando a metodologia Box-Jenkins e critérios informacionais para a estimação e validação do modelo; além disso, prever a evolução da variável fiscal para 2024. Uma vez identificado o modelo adequado com um ajuste praticamente perfeito —sendo este um SARIMA (1,1,1) X (1,0,1)12 —, a previsão para 2024 indica que a receita fiscal aumentará 4,73 % em relação a 2023 no mês de dezembro, considerando algumas causas possíveis deste comportamento. Em 2024, mantém-se uma espécie de ciclo de cobrança fiscal com picos no último mês, enquanto a atividade abranda nos restantes. Uma limitação desta investigação é a falta de consideração dos efeitos GARCH e das variáveis de controlo no âmbito da estimação, pelo que se recomenda que investigações futuras considerem estas directrizes.
Palavras-chave: fiscalidade, econometria, previsão económica, contribuições orçamentais, política fiscal.
JEL: H25. Impostos e subsídios sobre rendimentos empresariais.
Introduction
La recaudación tributaria en Ecuador es una de las principales fuentes de ingresos coactivos del Estado (Amaya 2014), la cual no cuenta con política monetaria desde inicios del siglo XXI. Los tributos sirven como instrumento de política económica general, estimulando la inversión, la reinversión, el ahorro y su destino hacia los fines productivos y de desarrollo nacional (EC 2018, art. 6).
La ponderancia de la recaudación tributaria en los ingresos estatales es primordial, dada la exclusividad de la política fiscal como herramienta para conseguir financiamiento público en el país. Según las operaciones del sector público no financiero, en 2023 los ingresos tributarios alcanzaron los USD 14 350,9 millones (12,08 % del PIB), que representa a su vez el 49,32 % de los ingresos no petroleros y el 32,91 % del total de ingresos.
Según el Servicio de Rentas Internas (SRI), la recaudación del Impuesto al Valor Agregado (IVA) en 2023 representó un 49,53 % de la recaudación bruta total del período, superando a su valor del período anterior (48,95 % de la recaudación bruta). De igual forma, según las estadísticas del Banco Central del Ecuador (BCE), la recaudación del IVA representó el 43,69 % del total de ingresos tributarios.
Ilustración 1 Ingresos tributarios trimestrales por IVA
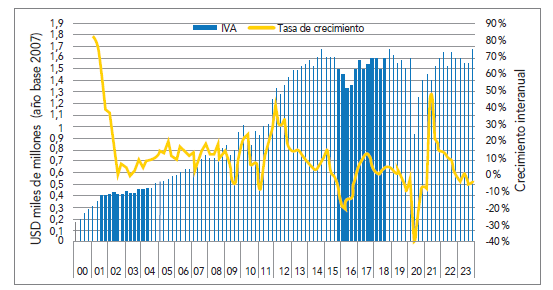
Elaboración propia a partir de los datos del BCE.
La tasa de gravamen del IVA se mantuvo desde la dolarización en 12 %, por lo que su análisis puede aplicarse de manera directa, más allá de las reformas estructurales referentes a las exenciones aplicables para los productos de primera necesidad. La recaudación en niveles sugiere a simple vista una especie de ciclo en los subperíodos: 2012-2015, 2016-2020 y 2021-2023. En dichos subperíodos, el cambio entre ciclos se debió a factores externos como la caída del precio del crudo o la pandemia de COVID-19.
Bajo esta línea de análisis, el nivel de recaudación tributaria constituye un componente importante dentro de la recaudación estatal, solamente por detrás de aquellos rubros correspondientes a la venta de crudo. A su vez, la recaudación tributaria responde, además de otros factores no económicos (Martin-Mayoral 2002), a shocks externos que afectan su nivel, como el de la emergencia sanitaria por la pandemia de COVID-19, en donde la recaudación tributaria descendió en más del 30 % con respecto a los valores de 2019 (Gómez Ponce 2020).
Para modelar y pronosticar impuestos importantes, se recomienda que los modelos autorregresivos integrados de media móvil (ARIMA) y sus derivaciones, tal como la consideración de la estacionalidad de los mismos (SARIMA), son métodos que deben utilizarse para la previsión de pagos futuros, pues resultan ser precisos en la previsión de ingresos fiscales, dado que estos minimizan los errores (Makananisa 2015).
El objetivo de esta investigación es desarrollar un modelo matemático bajo la metodología de Box-Jenkins de ARIMA/SARIMA, con el fin de predecir los ingresos fiscales generados por la recaudación del IVA causado para Ecuador en el período 2011-2023 por los grandes contribuyentes (GC) y un correspondiente pronóstico estático ex ante para los 12 meses de 2024, con el fin de asegurar la estabilidad política y presupuestaria. De manera equivalente, el pronóstico del modelo ideal será puesto a prueba frente a diversas alternativas fruto de la metodología propuesta. La calidad del pronóstico se evaluará mediante el coeficiente de desigualdad de Theil.
Marco teórico y estado del arte
Marco teórico: grandes contribuyentes
Los GC son aquellas personas naturales o jurídicas que representan más de la mitad de la recaudación tributaria en sus sectores, por lo que su tratamiento por parte de la administración tributaria es diferenciado. Se compone de los miembros relevantes de los grupos económicos, que abarcan sectores comerciales, productivos, financieros y de servicios.
Se usan los siguientes criterios, evaluados anualmente, para considerar a una persona natural o jurídica como GC:
-
Volumen y relevancia de las transacciones.
-
Aporte a la recaudación tributaria.
-
Comportamiento del sector económico al que pertenecen.
-
Monto del patrimonio.
-
Variables de riesgo y/o relevancia tributaria o económica.
Los GC se distribuyen geográficamente en un 50,14 % en la región Litoral (cuyo principal exponente es Guayas, con el 45,43 % del total de GC), 49,17 % en la región Interandina (Pichincha contiene el 44,57 % del total de GC) y el 0,29 % de la región amazónica (un solo GC en Zamora Chinchipe).
A su vez, los GC se componen de 200 personas naturales y 500 sociedades: el enfoque del presente artículo se centra en estas últimas.
Estado del arte
Los modelos ARIMA/SARIMA han demostrado ser herramientas robustas y versátiles en el análisis y pronóstico de series temporales en diversas disciplinas. Su capacidad para modelar datos que exhiben patrones de autocorrelación, tendencias y estacionalidades los hace especialmente útiles en contextos económicos y financieros. Una de las principales fortalezas de estos modelos es su flexibilidad para adaptarse a diferentes estructuras de datos temporales. Esto permite capturar dinámicas complejas en las series, mejorando la precisión de los pronósticos y facilitando la toma de decisiones informadas.
Diversos estudios han aplicado modelos ARIMA para pronosticar variables económicas clave. Por ejemplo, Tang et al. (2019) desarrollaron un modelo híbrido que combina ARIMA con máquinas de vectores de soporte optimizadas mediante algoritmos genéticos para predecir el índice de precios al productor (PPI) en China. Los resultados mostraron que este enfoque mejoró significativamente la precisión del pronóstico en comparación con modelos tradicionales.
Nkongolo (2023) exploró el uso de modelos ARIMA para predecir el consumo de datos de suscriptores en el sector de telecomunicaciones. La investigación destacó que ARIMA superó a modelos de redes neuronales convolucionales en términos de precisión y velocidad de ejecución, subrayando su aplicabilidad en la gestión de recursos y planificación de infraestructura en telecomunicaciones.
Uno de los estudios más representativos es el de Ayala y Bucio (2020), quien aplicó modelos ARIMA para analizar la evolución del tipo de cambio peso-dólar en el período 2016-2017 mediante ventanas temporales deslizantes. Los resultados indicaron que la volatilidad en la paridad cambiaria se debe a factores externos financieros, mientras que el modelo ARIMA permitió generar pronósticos a corto plazo con un alto nivel de precisión. Este estudio resalta la utilidad del modelo para analizar y predecir el comportamiento de monedas en mercados emergentes, especialmente en escenarios de alta incertidumbre económica.
Por otro lado, Dos Santos y Pacheco-Feria (2018) desarrollaron una investigación enfocada en el pronóstico de los precios del petróleo utilizando modelos ARIMA. Su estudio aplicó datos diarios del petróleo Brent, ajustando diversos modelos y seleccionando el que mejor minimizaba los errores de predicción. Los autores concluyeron que, si bien los modelos ARIMA ofrecen resultados robustos en la previsión de precios a corto plazo, la alta volatilidad de los mercados energéticos puede generar desviaciones en el largo plazo.
Otro enfoque relevante es el desarrollado por Gómez y Maravall (1994), quienes combinaron los modelos ARIMA con el filtro de Kalman para mejorar la estimación y predicción de series económicas no estacionarias. Su investigaci n evidenció que la integración de estos métodos permite una mayor precisión en la predicción de variables económicas altamente volátiles, como tasas de inflación y crecimiento del PIB.
En Ecuador, las recaudaciones fiscales juegan un papel muy importante dentro del gasto del gobierno; es por eso que el seguimiento y control de los ingresos tributarios resulta relevante para la óptima toma de decisiones de políticas. Según Luchko et al. (2021), se debe dar importancia a la previsión fiscal y a la modelación de los ingresos fiscales, porque de esta manera los decisores de política podrán lograr un sistema bien equilibrado; por ende, se debe acoger como parte de la gestión la modelación y pronóstico de dichos impuestos que aportan principalmente a los ingresos tributarios, a pesar de que algunos sucesos históricos se presencien en el futuro.
Asimismo, Jenkins, Kuo y Shukla (2000, 1) plantean que es necesario evaluar aspectos económicos, estructurales y políticos, supervisar la recaudación fiscal, analizar gastos tributarios y, finalmente, pronosticar los ingresos fiscales futuros para asegurar la estabilidad política y el presupuesto fiscal del Estado.
Un país debe modelar los ingresos fiscales con mayor precisión, pues de esa manera, la distribución presupuestaria estará más próxima a la realidad del futuro desconocido. Los modelos Holt-Winters y ARIMA/SARIMA funcionan bien para pronósticos de corto plazo; no obstante, tienen desventajas cuando se quiere explicar los componentes que influyen en la variable de interés (Pindyck y Rubinfeld 1997).
Meyler, Kenny y Quinn (1998) utilizan la modelación ARIMA de series de tiempo para pronosticar la inflación de Irlanda mediante la metodología de Box y Jenkins (1970), la cual cumple con el objetivo de la investigación: optimizar el pronóstico y minimizar los errores de pronóstico fuera de muestra, bajo el costo de sacrificar la bondad de ajuste dentro de muestra.
Büyükçahin y Ertekin (2019) indican que hacer pronósticos precisos es esencial para los tomadores de decisiones, donde los modelos de pronóstico de series de tiempo lineales y no lineales o una combinación de ambos pueden ser eficaces; sin embargo, dados los supuestos y restricciones que presentan estos modelos, se restringe el desempeño en ciertas situaciones, por lo que proponen el uso de un método híbrido de modelación ARIMA con redes neuronales artificiales. Hallan que esta modelación es una forma eficaz de obtener pronósticos precisos en un marco más general.
Luchko et al. (2021) buscaron sistematizar y analizar la metodología para la modelación de los ingresos fiscales causados por la recaudación del IR por importaciones; además, justificar la utilización del método de series de tiempo y lograr así un modelo ARIMA adecuado, mencionando que es relevante dar seguimiento y control a los ingresos tributarios. Hallaron que el IVA recaudado por importaciones tiene un impacto estadísticamente significativo en los ingresos fiscales; por tanto, elegir la mejor metodología que minimice pérdidas y prevea los ingresos fiscales en términos del IVA por importaciones, para realizar su modelación dentro de un país en transición o en desarrollo, tendrá un impacto significativo.
Materiales y métodos
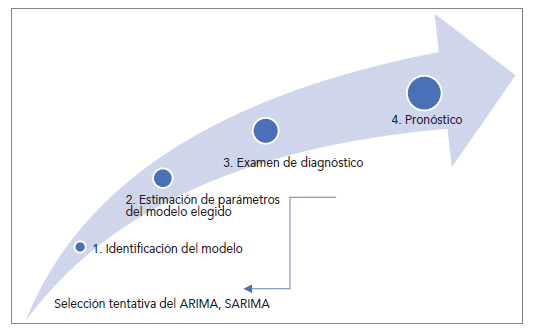
Con estos antecedentes, para modelar el comportamiento del IVA causado se utilizarán modelos econométricos estacionarios lineales, específicamente, los ARIMA y SARIMA; esto siguiendo la metodología propuesta por Box y Jenkins (1970), que consta de cuatro pasos (ver ilustración 2).
En el primer paso, se deben plantear modelos tentativos que parezcan explicar de mejor manera la data, eligiendo el de mejor ajuste; para este fin, se construyen los correlogramas simple (FAC) y parcial (FAP). Luego, se estiman los parámetros y los residuos del modelo elegido; si estos residuos son ruido blanco, se avanzará al pronóstico; caso contrario, se deberá regresar al primer paso e iniciar el proceso nuevamente.
Una serie temporal Yt es estacionaria si "su distribución de probabilidad no varía en el tiempo, es decir, si la distribución conjunta de (Ys+1, Ys+2,..., Y s+t ) no depende de s (rezago), sea cual sea el valor de T; de lo contrario, se dice que es no estacionaria" (Stock y Watson 2011, 387).
Procesos autorregresivos integrados de media móvil (ARIMA)
Estos procesos se representan como ARIMA (p, d, q), es decir, un proceso autorregresivo de media móvil de orden (p, q) que debió ser diferenciado d veces para convertirse en un proceso estacionario, donde el término p representa el mayor orden de los rezagos autorregresivos y el término q el mayor orden de rezagos de procesos de media móvil. De manera compacta, se expresa de la siguiente manera:
Procesos estacionales autorregresivos integrados de media móvil (SARIMA)
Son una extensión del proceso ARIMA, generalmente utilizados en la modelación de series cronológicas que muestran un patrón estacional. Una ventaja significativa es que superan la incapacidad de los modelos ARIMA en la representación precisa de los correlogramas (FAC y PAC) en procesos estacionales.
La serie se escribe de la siguiente manera:
En donde: D representa el número de diferenciación estacional y s representa la temporalidad.
A diferencia de los modelos ARIMA en las funciones de autocorrelación, o correlogramas, este proceso presenta fuertes incrementos en torno a los rezagos asociados a la estacionalidad de la serie.
Pincheira y García (2009) destacan importantes ventajas de la modelación SARIMA al incorporar directamente el patrón estacional de una serie, sin separar los componentes estacionales y no estacionales.
Validación del modelo
En general, se busca que los modelos propuestos y estimados cumplan con estándares mínimos de calidad y ajuste; por ello, en primer lugar, hay que verificar que las perturbaciones sigan un proceso de ruido blanco, es decir, mediante el test multivariante de Portmanteu (Johnston y DiNardo 1996).
Para seleccionar entre los distintos modelos planteados, es ventajoso utilizar los criterios informacionales Akaike (AIC) y Schwarz (SBC), donde el menor valor de estos criterios indicaría el modelo adecuado (Koehler y Murphree 1988). Además, se evalúan los pronósticos utilizando el coeficiente de desigualdad de Theil (Pindyck y Rubinfeld 1997).
Tabla 1 Patrones teóricos en los correlogramas del proceso ARIMA
Fuente: Gujarati y Porter (2009). Elaboración propia.
Datos
Se emplea la serie cronológica mensual de los GC en el período enero 2011-diciembre 2023, de acuerdo a los datos del SRI (ilustración 3).
Ilustración 3 IVA causado por los GC durante el período 2011-2023
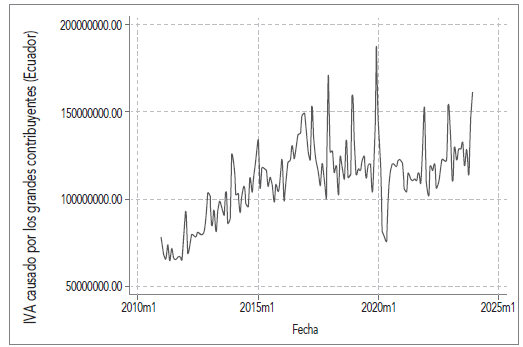
Elaboración propia a partir de los datos del SRI.
Al analizar el comportamiento, se evidencia hasta 2017 la posible presencia de una tendencia determinística creciente con cierta volatilidad, es decir, una recaudación creciente con el tiempo, lo cual concuerda con la evolución de la recaudación del IVA a nivel general hacia 2015. Desde 2017, se presenta cierta estacionariedad en media con mayor volatilidad, lo que significa que, si bien los picos alcistas presentan niveles de recaudación astronómicos, la tendencia desde 2017 parece implicar que la recaudación por IVA causado a GC no ha variado significativamente, lo cual entra también en concordancia con el crecimiento nulo de la recaudación de este impuesto a nivel general.
La serie en general presenta cierto patrón repetitivo con picos altos en diciembre de cada año, lo que daría evidencia de un componente estacional. Este comportamiento se justifica dado que las sociedades que conforman los GC tienden a declarar sus impuestos semestralmente, elevando así los montos recaudados en los meses de junio y diciembre. Mención aparte merece el aumento notorio en el último trimestre de 2019 y la caída abrupta a inicios de 2020: los shocks producidos por la declaratoria de emergencia por la pandemia en el país y la consecuente caída en la actividad económica fueron situaciones extremas que el modelo propuesto no pudo recoger en su totalidad.
Resultados
Como paso previo, se determinó que el IVA causado no es estacionario en media de acuerdo con el test de Dickey Fuller. 1 Sin embargo, existe evidencia de perturbaciones autocorrelacionadas, siendo significativo incluso al rezago 12; 2 en lo que respecta a la heteroscedasticidad, el test de Breusch-Pagan indica que la varianza es constante. 3
Por la presencia de autocorrelación en los shocks, resulta más adecuado implementar el test Dickey Fuller aumentado (ADF). Para ello, se siguió el procedimiento secuencial de Mahadeva y Robinson (2004), comprobando que el IVA causado posee raíz unitaria, es decir, no es estacionaria (considerando once rezagos, sin tendencia ni intercepto).
Tabla 2 Test de Dickey Fuller aumentado
| Test | Valores críticos | |||
|---|---|---|---|---|
| Statistic | 1% | 5 % | 10 % | |
| Z(t) | 1,858 | -2,596 | -1,950 | -1,613 |
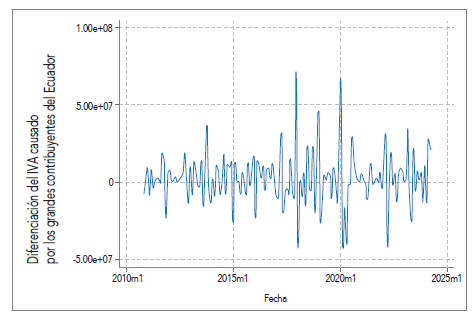
A partir de esto se obtuvo el orden de integración I (1) 4 , por lo que se necesita diferenciar una vez la serie para que se vuelva estacionaria. Se observa la estacionariedad en media del IVA causado en la ilustración 4, mas no en la varianza.
De acuerdo con Mauricio (2007), para estabilizar la dispersión se utiliza una transformación de Box-Cox, sustentada en la obtención del parámetro λ. Como la desviación estándar resultó ser proporcional a la media en nuestra variable de interés, es decir, λ = 0, la transformación adecuada es el logaritmo natural. 5
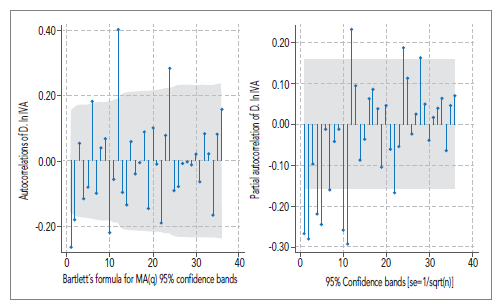
En este sentido, se obtuvo el logaritmo natural del IVA, y su primera diferenciación, para convertir la serie en estacionaria tanto en media como en varianza; por lo que se procedió a aplicar la metodología Box-Jenkins. Para proceder a la identificación del modelo, fue necesario construir los correlogramas simple (FAC) y parcial (PAC) de la serie estacionaria (ilustración 5).
Al dar lectura al PAC y FAC, se proponen diversos modelos ARIMA: mediante una comparación estadística se determinó que el modelo ARIMA (1, 1, 1) es el apropiado. 6
Sin embargo, al inspeccionar el comportamiento de las perturbaciones, estas no siguen un proceso de ruido blanco, de acuerdo con el test de Portmanteu; 7 para poder capturar los rezagos que podrían estar generando esta anormalidad en los residuos, se utilizan modelos SARIMA, 8 resultando en que el modelo SARIMA (1,1,1) (1,0,1)12 es el apropiado, siendo la estimación del IVA causado por GC, en logaritmos, (iva t ):
Donde L representa el operador de rezagos.
Con estos resultados se realizó una proyección estática; aunque el modelo seleccionado evidenció una capacidad adecuada para identificar tanto los picos alcistas como los bajistas, exhibió ineficacia al capturar variaciones extremas (ilustración 6).
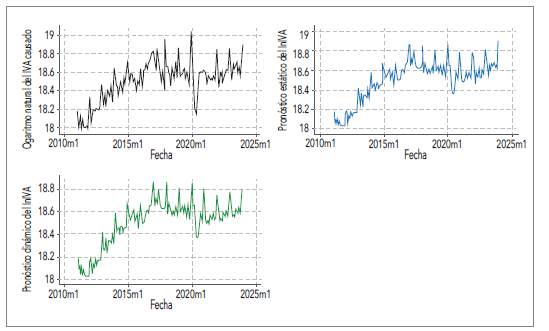
Ilustración 6 Predicción del IVA causado por los GC bajo el modelo SARIMA propuesto
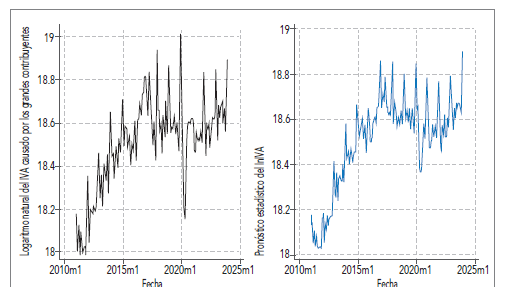
Elaboración propia.
En la mera práctica, se encontró evidencia de efectos ARCH/GARCH según el test formal, 9 es decir, se tendría evidencia de heterocedasticidad condicional y volatilidad agrupada en la serie. Sin embargo, se calculó el coeficiente de desigualdad de Theil, correspondiente al pronóstico dinámico ex post, 10 que arroja un ajuste prácticamente perfecto del modelo propuesto.
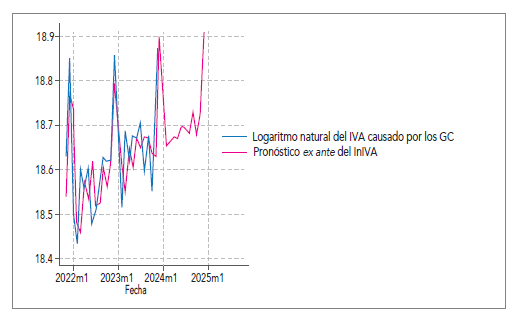
Con ello, finalmente, se procede a realizar un pronóstico ex ante hasta diciembre de 2024, obteniendo los resultados que constan en la ilustración 7.
Para transformar el pronóstico en niveles, se puede utilizar la función exponencial, sin embargo, Wooldridge (2009) menciona el disfuncionamiento de esta, pues termina subestimando de manera sistemática el valor esperado de la variable de interés. Para ello se plantea un sencillo ajuste representado por:
Donde σ2 representa la varianza incondicional del proceso SARIMA. La predicción resulta:
Tabla 3 Pronóstico para el IVA causado por GC en 2024, en dólares
Discusión y conclusiones
La modelación y pronóstico del IVA causado por los GC resulta importante para la toma de decisiones presupuestarias, considerando que los ingresos permanentes, como el IVA, financiarán los egresos permanentes (EC 2008, 286).
En este sentido, se halló que el comportamiento presenta un componente estacional, el mismo que se evidencia con aumentos en el monto de recaudación en junio y diciembre, lo que se corrobora con la frecuencia de declaración de los GC y la naturaleza de la política tributaria, donde dichos meses son próximos a la declaración semestral de bienes y servicios con tarifa 0 %.
El pronóstico del IVA causado indica que para 2024 se mantendrá la tendencia de un pequeño ciclo recaudatorio, que a inicios y finales del año experimenta grandes cuantías en la recaudación, y el resto de los meses mantiene una posición más discreta, incluido junio, que es cuando se hace la primera declaración semestral. El Gobierno puede aplicar incentivos para una mayor recaudación del IVA para los GC, así como para una menor volatilidad, a fin de aumentar la recaudación fiscal y mejorar las cuentas públicas.
Factores endógenos de envergadura podrían afectar las recaudaciones, tal como se evidencia en el período de la pandemia del COVID-19, por lo que la metodología propuesta es una herramienta útil para la entidad tributaria y los policy makers para asegurar estabilidad en las finanzas públicas.
Por otro lado, el pronóstico realizado para 2024 indica que existiría un aumento promedio del 4,73 % en la recaudación tributaria de los GC con relación al año anterior (ver tabla 4). La recaudación del primer semestre es relativamente débil en comparación con la de finales de año, en donde se auguraría un aumento de cerca de USD 20 millones en la recaudación tributaria de los GC.
La tasa de variación interanual pronosticada para 2024 indicaría una ligera ralentización de la tributación ecuatoriana con respecto a los dos últimos años, lo cual también se complementa con el promedio estable de la recaudación desde 2017. Esta clase de estancamiento del IVA causado por los GC indica fuertes alarmas para la entidad tributaria, y entre las causas indirectas de este comportamiento están: 1. no se han constituido más GC, 2. la declaración de IVA de dichas sociedades no se altera significativamente con respecto al año anterior por la invariabilidad en la ley de recaudación tributaria, 3. los ingresos de GC no han variado significativamente, y 4. la cultura tributaria de estas sociedades puede caer en evasión tributaria (Fanelli 2009). Se recomienda que estas hipótesis sean corroboradas en futuras investigaciones, dado que el trasfondo de estos resultados es inobservable en estos datos temporales. Una sugerencia sería utilizar modelos que ayuden a comprender, medir y gestionar este fenómeno, como por ejemplo los modelos ARCH, GARCH y EGARCH, ya que permiten modelar la volatilidad y proporcionar información útil para la toma de decisiones.
Tabla 4 Variaciones porcentuales promedio de la recaudación del IVA
En el período de análisis, la tarifa del 12 % y la mayoría de los bienes y servicios gravados se mantuvieron estables, es decir, la normativa tributaria no sufrió mayores cambios y el empleo de esta metodología es apropiado. Sin embargo, desde abril de 2024, el aumento del IVA en un 3 % abre un nuevo panorama en el que, dependiendo de los factores económicos, la recaudación tributaria a nivel general y con los GC puede experimentar cambios más disruptivos, con lo cual se deberá emplear nuevas metodologías y herramientas.
NOTAS
[5] Véase anexo 1.
[6] Véase anexo 2.1.
[7] Véase anexo 2.2.
[8] Véase anexo 4.
[9] Véase anexo 4.
[10] Véase anexo 5.1.
[11] Véase anexo 5.2.
[12] Véase anexo 6 para la estimación de modelos.
[13] Véase anexo 7.
[14] Véase anexo 8.
[15] Los autores declaran haber cumplido con los principios éticos durante el proceso de investigación
[16] Erick Galarza Molina participó en la conceptualización, curación de datos, análisis formal, investigación, metodología, administración del proyecto, recursos, software, supervisión, validación, redacción del borrador, redacción, revisión y edición del artículo final Alfredo Loja Villalta participó en la conceptualización, curación de datos, análisis formal, investigación, metodología, administración del proyecto, recursos, software, supervisión, validación y redacción del borrador, redacción, revisión y edición del artículo final. Patricio Baculima Cuesta participó en el análisis formal, investigación, metodología, validación, visualización, redacción del borrador. Karla Sigüenza García participó en el análisis formal, investigación, metodología, validación, visualización y redacción del borrador.
Appendices
Anexos
Anexo 2. Test de autocorrelación y heterocedasticidad
Tabla 6 Test de autocorrelación de Breusch-Godfrey
Anexo 5. Proceso autorregresivo integrado de media móvil (ARIMA) de orden, (p, d, q), ajustado para el IVA causado por los GC
Tabla 10 Estimaciones Procesos ARIMA, IVA c
Al examinar los coeficientes estimados de cada uno de los procesos, se observa significancia estadística. Considerando el principio de parsimonia y los criterios informacionales, se concluye que el modelo más adecuado es un ARMA (1, 1, 1).
Anexo 6. Procesos estacionales autorregresivos integrados de media móvil de orden (p, d, q) (P, D, Q)12, ajustado para el IVA causado por los GC
Tabla 12 Estimaciones procesos SARIMA, IVA c