Introducción

Existen varias maneras de realizar un plan óptimo de producción, sin importar la clase de industria; estas técnicas de modelar o programar la producción buscan, por lo general, optimizar o incrementar sus ganancias a través de modelos matemáticos relacionados con la investigación de operaciones (Herrera 2011), la cual consiste en la aplicación de un método científico que se basa en un enfoque sistémico, cuyo objetivo es producir las mejores alternativas de solución para la toma de decisiones (Ortiz y Olivares 2015).

Uno de los elementos principales a considerar en la investigación de operaciones es el modelo matemático que esta ciencia genera conforme a lo que el modelador desea hacer (Taha 2012). Aunque existen otras metodologías para la resolución de este tipo de estudios (Hillier y Hillier 2008), es fundamental resaltar la importancia de la técnica de programación lineal, aclarando que la palabra lineal se refiere a la forma de las expresiones matemáticas en este tipo de modelo; y, programación no se trata de ejecutarlo en computadora, sino que se utiliza como sinónimo de planeación. De esta manera, programación lineal significa la planeación de actividades que se representa mediante un modelo matemático (Alvarado 2009).

En tal virtud, el modelo matemático planteado para este caso de estudio refleja la importancia de la investigación de operaciones aplicado en una empresa real, cuyo objetivo fundamental es proveer una herramienta de continua aplicación sin importar el tiempo en el cual es utilizado.

La metodología aplicada en conjunto con la teoría de las restricciones (TOC) posibilita que el modelo sea de continua aplicación, aprovechando que la TOC es un proceso que puede aplicarse en conjunto con la metodología de la programación lineal, fundamentalmente en la generación de las restricciones del modelo.

Por lo tanto, al obtener los resultados mediante la aplicación de la programación lineal, es factible definir su planeación agregada para encontrar los costos de producción, cuyos resultados servirán de insumo para reflejar los diversos escenarios productivos que se pueden presentar (Reyes et al. 2017).

Revisión de literatura

A lo largo del tiempo han existido diversos estudios realizados en distintas empresas. Dentro de estos estudios se encuentra el realizado en una planta embotelladora de gaseosas que utiliza la técnica de la programación lineal junto con la teoría de las restricciones (TOC), obteniendo un modelo matemático que permitió lograr cantidades óptimas de fabricación al menor costo posible, en un período, en el cual la cantidad de recursos no es ideal para obtener mejores resultados (Ortiz y Caicedo 2012).

De conformidad con lo detallado, Eppen et al. (2000) señalan que la cantidad óptima de producción de cada elemento a obtenerse constituye el plan óptimo. Estos planes de producción, en general, deben considerar las restricciones para el detalle manufacturero que se desee elaborar o diseñar; adicionalmente, es necesario analizar qué cantidades se requiere y los tiempos de entrega de dichos artículos (Sipper, Bulffin y González 1998).

Este modelo en el que los autores utilizan la teoría TOC, es una técnica aceptable para elaborar modelos matemáticos dentro de la programación lineal, evidenciando que algunos de ellos tienen menor capacidad de utilización o producción que otros (Krajewsky, Ritzman y Malhotra 2008).

Lo expuesto es corroborado por Motta y Silva (2016) quienes, a través del diseño de un modelo de programación lineal difuso, logran planificar la programación de la producción para envases de vidrio, minimizando el tiempo empleado en los estándares productivos. Otro estudio ejecutado es el modelo de programación óptimo para la producción en una pequeña empresa de calzado, que posibilita obtener cantidades óptimas de fabricación para un semestre determinado, maximizando el ingreso económico (Ortiz y Caicedo 2014).

Lo detallado está en concordancia con lo especificado por Singer (2017), quien precisa que las variables que utiliza un modelo de programación lineal cuantifican las decisiones a ser tomadas. De la Hoz, Vélez y López (2017), presentan un modelo de programación lineal multiobjetivo aplicado a una empresa en el sector del plástico, su principal aporte es la revisión de los referentes teóricos relacionados con el proceso de recuperación del plástico de polipropileno.

Barboza, Mendoza y Fariña (2019), realizaron el estudio de programación lineal aplicada al despacho de carga en Paraguay, en el cual describen las ecuaciones de un problema de optimización para el despacho de carga de las centrales de generación eléctrica que abastecen al sistema interconectado de dicho país, mediante la utilización de las herramientas Optimization Toolbox y MatLab, cuya finalidad fue verificar el comportamiento satisfactorio del algoritmo utilizado.

De la misma manera Romero-Rojas, Ortiz-Triana y Caicedo-Rolón (2019) describen un caso de estudio en una industria de muebles, en la cual utilizan la teoría de restricciones en conjunto con la programación lineal, aplicando enfoques contables empleados en la teoría de las restricciones, considerando para aquello la contabilidad del Throughput Accounting (TA). Complementariamente, Geri y Ahituv (2008) señalan que esta metodología es una heurística de fácil entendimiento para aplicarse en casos de producción y útil para soportar la toma de decisiones.

Robles (2017) presenta un modelo de optimización para una cadena de suministros, que facilita la toma de decisiones mediante la construcción de un modelo de programación lineal entera mixta, incorporando un indicador ambiental de emisiones de carbono para valorar y afrontar el cambio climático. Adicionalmente, Canseco et al. (2016), ejecutan un modelo que busca optimizar la asignación de recursos en determinados períodos con requerimientos puntuales, utilizando la técnica de ramificación y acotamiento disponible mediante el uso del sistema informático Lingo.

Bajo la misma perspectiva, otros autores diseñaron y resolvieron tres modelos matemáticos utilizando programación estocástica multietapa; inicialmente, abordaron un plan agregado de manufactura para diversos productos y, para los restantes, manejaron un plan de producción para analizar las mejores decisiones que debían tomarse (Albornoz y Ortiz-Araya 2010).

Al presentarse la posibilidad de diseñar un modelo matemático para cualquier industria utilizando programación lineal, en una planta extrusora de tubos se consideraron variables como: tiempos de producción por especificaciones de cada tipo de tubo y extrusora y las capacidades semanales de producción en cada una de las extrusoras conforme a las unidades producidas; logrando una representación óptima del proceso productivo para la fabricación de tubos de policloruro de vinilo o PVC (Krastek, Ramos y Duarte 2012).

Silva, Díaz y Galindo (2017) realizaron un análisis para mostrar las tendencias de diversas investigaciones relacionadas con la planeación y programación de la producción utilizando la programación lineal, programación lineal entera mixta, algoritmos, métodos de aproximación y programación estocástica, con lo cual evidencian que, a pesar de no haberse aún divulgado en la proporción deseada el diseño de modelos matemáticos a través de la aplicación de la disciplina de la investigación de operaciones, ha incrementado notablemente su uso en los últimos cinco años, ubicándose en un 58 % en relación a la década de los años 2001-2010, cuando únicamente se utilizaba un 18 %.

Al realizar la revisión bibliográfica de cada uno de los trabajos efectuados por los autores mencionados, es notable señalar que el diseño de estos modelos se encuentra, en algunos casos, complementados con la ejecución de la planificación de la producción, utilizando para aquello la metodología denominada planeación agregada, la cual se integra eficazmente con la programación lineal. Linfati, Pradenas y Ferland (2016), ejecutaron un estudio en el cual inicialmente se planteó un modelo de programación entera mixta para la planificación táctica de la cosecha forestal, combinando eficazmente la programación lineal entera mixta con la planeación agregada, considerando hasta 260.000 variables, 4800 enteras y 10.000 restricciones usando el software Cplex.

La industria farmacéutica no queda al margen de la aplicación de estas metodologías. Pacoricuna y Mejía (2015) elaboraron un modelo para una industria farmacéutica en Lima; se concentraron en estudiar la línea de producción de líquidos no estériles, con el objetivo de mejorar los costos de horas-hombre en el proceso de producción. Moniz, Barbosa-Povoa y Pinho de Sousa (2015) elaboraron un modelo para una industria químico-farmacéutica, en la cual la programación de la producción utiliza un enfoque de horizonte variable y estrategias de reformulación y ramificación, para tratar la complejidad computacional del problema. Viera et al. (2016), en cambio, realizaron un trabajo de optimización en la programación de los procesos de fabricación biofarmacéutica, considerando varias características operativas para lo cual desarrollaron un modelo de programación lineal de enteros mixtos.

Ríos y Contreras (2018) elaboraron una investigación sobre rendimientos a escala en la industria farmacéutica mundial, la cual no está dirigida específicamente a la gestión de la producción, pero diseñaron un modelo matemático para analizar los resultados en función de los gastos incurridos en investigación y desarrollo (I+D) y otros gastos operacionales.

Con base en lo especificado, la planeación de la producción utilizando programación lineal mediante el diseño de un modelo matemático, no siempre va acompañada del conocimiento del personal que planifica la producción en una empresa, por el desconocimiento de las herramientas que faciliten su implementación, encontrándose varios inconvenientes relacionados a la fuerza laboral, instalaciones, sistemas y tecnología (Carro y González 2012).

En tal virtud, en la planta farmacéutica, sujeto de estudio, en la sección de producción de soluciones parentales (sueros), antes de iniciar su proceso productivo, la programación de la producción se realiza con base en datos históricos de productos generados en una jornada laboral específica, o en el plan de ventas estipulado por el departamento correspondiente, apoyándose en la experiencia del personal que trabaja en dicho proceso, personas que no están familiarizadas con los métodos de optimización.

Es importante recalcar que en Ecuador el 80 % de las medicinas son importadas. Esta diferencia también se evidencia en los volúmenes de venta, es así como, de los USD 1500 millones que mueve el sector farmacéutico en el país, USD 1000 millones corresponden a medicina o medicamentos importados (Armijos 2014).

Por lo tanto, la programación de la producción apoyada en modelos matemáticos ayuda a la empresa a mejorar sus planes productivos, respondiendo con mayor rapidez las solicitudes de los clientes y creando programas realistas. Pero, aun así, una de las principales dificultades podría no radicar en el diseño del modelo o en la programación de la producción propiamente dicha, sino en su implementación (LaForge y Craighead 1998).

El objetivo de esta investigación es el diseño de un plan óptimo de producción en una planta farmacéutica que produce soluciones parentales (sueros) para facilitar el conocimiento de las cantidades óptimas a producir, lo que permitirá a la empresa que, ante las necesidades de los clientes y organizacionales, satisfaga sus requerimientos considerando la metodología de la programación lineal complementado con la planeación agregada.

Metodología

La empresa, que es la unidad de análisis, es una organización farmacéutica que cuenta con su planta de producción. La producción de las soluciones parentales se enfoca en productos de presentaciones relacionadas a 1000, 500, 250 y 100 ml. Para alcanzar el objetivo propuesto en esta investigación, se desarrolló un programa óptimo de producción aplicando la programación lineal y la planeación agregada complementada por la teoría de las restricciones, las cuales en conjunto facilitan evidenciar metodológicamente el tipo de investigación denominado caso de estudio. Bernal (2010) señala que el caso de estudio se utiliza ampliamente en los campos relacionados a la economía y administración, posibilitando estudiar en detalle una unidad de análisis específica comprendido como un sistema integrado que interactúa en un contexto concreto con características propias.

Esta conceptualización fue aplicada en la línea productiva de soluciones parentales en un mes específico (febrero 2020), que fue seleccionado por la similitud de producción con el resto de los meses, logrando generar un modelo que pueda replicarse en cualquier período. Las fases principales para el diseño de este modelo se desarrollaron con base en la investigación de operaciones, lo cual se visibiliza en la figura 1.

Es importante especificar que la investigación de operaciones no se limita a una sola técnica general con la cual se puedan resolver todos los modelos matemáticos que surgen en la práctica (Taha 2012). Lo expuesto es corroborado por Mathur y Solow (1998), quienes señalan que el proceso inicialmente identifica, entiende y detalla en términos precisos el problema que la organización o empresa enfrenta. Considerando especialmente que, si la solución no se puede llevar a cabo, es posible identificar las limitaciones que se omitieron, o revisar si las restricciones planteadas fueron las correctas.

Figura 1
Metodología de resolución de modelo planteado

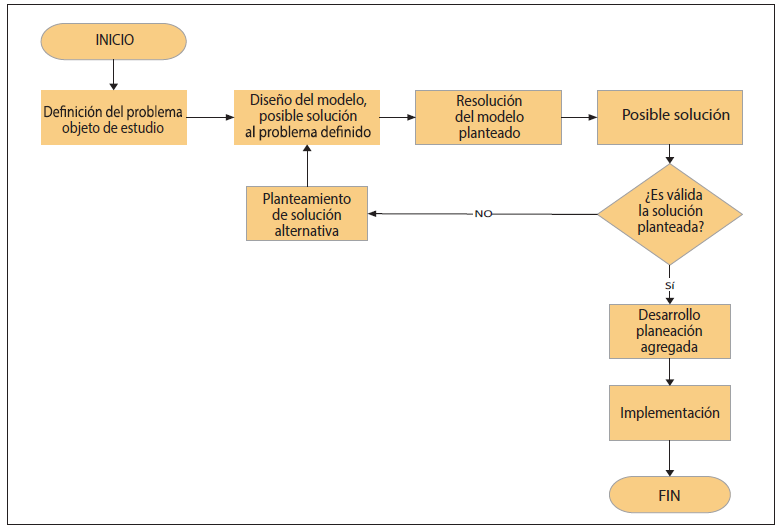
Elaboración propia.

A modo específico, el modelo diseñado en su fase de planteamiento conforme a la metodología de la programación lineal cumple con las siguientes fases:

• Definición de las variables del problema.
• Definición de la función objetivo.
• Establecimiento de las restricciones.
• Obtención de resultados.

En el paso del establecimiento de las restricciones, el estudio se complementa con lo señalado por la teoría de las restricciones (TOC por sus siglas en inglés), teoría diseñada por Goldratt y Cox (2008) quienes especifican cinco pasos que se relacionan entre sí y pueden considerarse como un ciclo continuo: identificar las restricciones, explotar dichas restricciones, subordinar todo a la restricción principal, elevar la restricción y, al lograr romper la restricción, volver al paso inicial.

Desarrollo del modelo

En la actualidad, la empresa considera que sus recursos no son utilizados eficientemente en la fabricación de las soluciones parentales, pero sí buscan una mayor producción sin emplear recursos adicionales.

Variables que intervienen en el proceso productivo
de soluciones parentales (sueros)

Las variables que intervienen en el modelo vienen dadas por:

Xab: cantidad de cajas a fabricar por producto (a) en un determinado período (b).

Para el diseño del modelo se considera que, sin importar el producto o solución parental (suero) que se fabrique, están acompañados de constantes que entre sí forman las restricciones necesarias para el planteamiento del modelo matemático. Estas variables, al utilizarse en la fabricación de cada uno de los productos, están en función de: costo de fabricación, demanda, envase para el producto, tiempos requeridos, capacidades de producción mínimas y máximas de soluciones y la capacidad total de preparación del producto.

En la tabla 1 se detallan las variables utilizadas para la generación del modelo planteado:

Tabla 1
Variables utilizadas para el planteamiento del modelo

Elaboración propia.

Es importante anotar que en los períodos de fabricación de cada producto se consideran los tiempos utilizados para la preparación de: llenadoras, bandas transportadoras, esterilización de autoclave, preparación de envases (fundas), así como también los tiempos de esterilización de tuberías, tiempo de llenado de cada unidad (sueros), tiempo de generación de agua destilada, tiempo de impresión de precio en producto envasado, encartonado y entrega a bodega de cada lote producido. Estos parámetros ingresarán en la variable correspondiente al tiempo requerido para la fabricación de producto (TPa).

Función objetivo

La función objetivo (Z) busca minimizar los costos de producción en función de las restricciones planteadas:

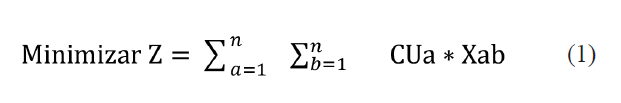
Restricciones

Restricción de capacidad de llenado

Esta restricción se plantea en función de los tiempos encontrados en sitio, acorde al trabajo que realizan los trabajadores en la empresa:

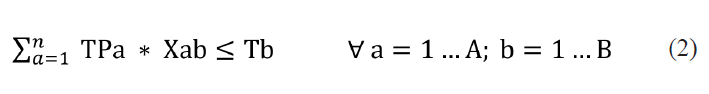
Restricción de demanda

La restricción de los datos de la demanda fueron proporcionados por el proceso de producción, considerando para ello la demanda general del producto.

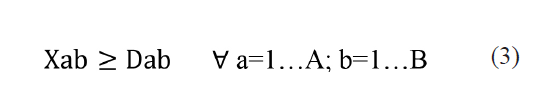
Restricción de disponibilidad de envases (fundas) para el llenado

Planteada en función de los datos proporcionados por las áreas de producción y almacenamiento de la compañía.

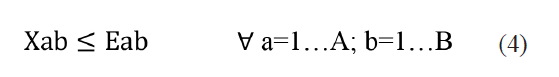
Restricción de capacidad de preparación de la solución parental (solución inicial)

Considera la capacidad máxima y mínima que el proceso posee para la preparación inicial de la solución.

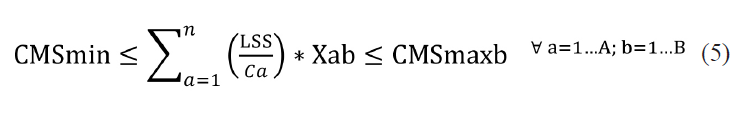
Restricción de capacidad de preparación lote terminado (solución final)

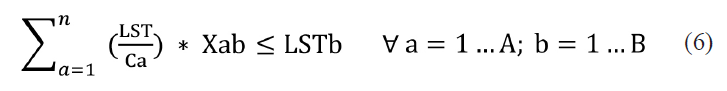
Los valores de esta restricción se determinaron mediante el cálculo del número de preparaciones disponibles en el período estudiado.
Por último, la restricción de no negatividad de la variable principal del modelo:

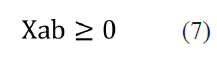
El modelo matemático diseñado es acorde a la función objetivo y a las restricciones planteadas. La implementación de estas restricciones en conjunto con su función objetivo posibilita obtener el número ideal de unidades a producir, dicho número de unidades posibilita determinar los costos totales mediante la aplicación de la técnica denominada planeación agregada.

Resultados

De acuerdo con el planteamiento de la función objetivo, de las restricciones planteadas y los datos recopilados en el sitio, el modelo matemático diseñado utilizando la metodología de la teoría de las restricciones en conjunto con la programación lineal, permite obtener soluciones en las cuales se evidencia la mejora de los resultados que puede alcanzar el proceso productivo de soluciones parentales (sueros).

Para lo planteado se considera que las restricciones de llenado y preparación de las soluciones hacen referencia a los recursos productivos de la empresa posibilitando que la solución propuesta permita alcanzar los objetivos mediante una correcta utilización de dichos recursos, ya que, al menos de manera explícita, no contaba con una herramienta metodológica que lo permita.

Adicionalmente, este estudio contribuye directamente al conocimiento científico mediante la aplicación en sitio de un modelo matemático diseñado para el efecto; dicho modelo se lo desarrolló en función de los datos generados y establecidos inicialmente conforme a los requerimientos de la empresa. El estudio presenta un análisis de la utilización de los recursos, considerando para ello el mes de febrero de 2020, facilitando apreciar la existencia de tiempos y capacidades no utilizadas adecuadamente. Además, fue posible identificar las actividades esenciales de producción donde se generan los mayores retrasos, logrando identificar los porcentajes de capacidad no utilizada (tabla 2).

Análisis de recursos

En el modelo propuesto es importante recalcar que la demanda es la restricción limitante, por cuanto no se la considera en función de las ventas del producto sino que se la estudia en función de la demanda del mercado en la ciudad de Quito. Por tal motivo, se puede afirmar que la producción de la empresa es menor a dichas necesidades; por lo tanto, la organización debe asegurar la producción adecuada para satisfacer las solicitudes de sus clientes. Con esta pequeña introducción, se lleva a cabo un estudio de métodos y análisis de cargas de trabajo, con el cual se buscó incrementar la productividad considerando que esta metodología puede ser aplicada a cualquier tipo de organización (Rojas, Correa y Gutiérrez 2012), identificando para el efecto que la actividad de llenado de las soluciones presenta las mayores dificultades en tiempos de demora dentro de la línea productiva, y determinando que la capacidad no utilizada de dicha actividad se ubica en el 25 %.

Tabla 2
Análisis de la utilización de recursos

Fuente y elaboración propia.

De acuerdo con los valores determinados, otro de los aspectos importantes a examinar es que el modelo propuesto considera que la organización posee un nivel mínimo de inventario, el cual, de la misma manera, no excede a la demanda. Este inventario al ser fijo en una determinada cantidad dependiendo de las unidades producidas para el modelo propuesto, se considera un valor de cero con lo cual se obtendrá un valor específico de producción para cada uno de los productos que la empresa comercializa.

Lo expuesto se respalda en los criterios de Berruto, Tortia y Gay (2006), quienes elaboraron un modelo de optimización de la programación del embotellado de vino considerando el aspecto del inventario en un valor inicial de cero, principio utilizado para la generación de dicho modelo; este enfoque es aplicable de igual forma en este estudio. En tal virtud y acorde a lo señalado en líneas anteriores, considerando que la producción no presenta una actividad que detenga el proceso más allá de una capacidad no utilizada el modelo propuesto, se analiza en el software WinQSB para Windows, versión 5.2.

Se conoce con certeza que no se puede llenar la solución parental más allá de lo planificado por la empresa, considerando que el laboratorio farmacéutico debe asegurar la disponibilidad del envase (fundas) para dar cumplimiento a las solicitudes de los clientes que, acorde a la TOC, la prioridad principal es explotar al máximo la capacidad de llenado disponible. En consecuencia, se determinan las cantidades óptimas de producción requeridas para el mes de estudio (febrero 2020), recalcando que la producción ideal encontrada está determinada en función de un lote de producción (tabla 3).

Tabla 3
Número de unidades de producción ideal en el mes de febrero de 2020

Fuente y elaboración propia.

Se ejecutó un comparativo con Berruto, Tortia y Gay (2006), y se obtuvo que el número ideal de producción está en función de la cantidad ideal a producir por lote, sin importar el producto que se desea fabricar, lo que permite a la empresa programar su producción acorde a las necesidades del proceso de comercialización al aplicar el modelo diseñado, de acuerdo con las restricciones planteadas, la capacidad de producción no utilizada y considerando a la restricción de la demanda como aquella a la cual el modelo podría explotar para analizar diversos escenarios. En la tabla 4, se presentan estos escenarios, los cuales se ejecutan de una manera aleatoria, buscando lograr los valores ideales de producción especificados en la tabla 3, sin necesidad de utilizar recursos adicionales.

Tabla 4
Escenarios posibles de incremento

Elaboración propia.

Al visualizar el comportamiento de los recursos productivos mediante el análisis de escenarios, se evidencia que el sistema productivo realiza un aprovechamiento de recursos de manera óptima, diferente al que actualmente presenta la organización. Estos incrementos en los escenarios propuestos alcanzan los resultados descritos en la tabla número 5.

Tabla 5
Análisis de la utilización de recursos al incrementarse la producción en un 28,5 %

Elaboración propia.

Al determinar el número ideal de unidades que deberían producirse conforme a los resultados evidenciados en la tabla 3, se presenta a continuación la planeación agregada de la producción posibilitando encontrar su costo económico total.

Costos de implementación

Acorde a lo señalado en las anteriores líneas, es posible determinar el costo de implementación de estos resultados mediante la utilización del sistema informático Lingo en su versión 15.0.

Para esta planeación agregada se considera únicamente los productos parentales en su presentación de 1000 ml con lo cual el modelo planteado podrá utilizarse acorde a las necesidades de la empresa. Esta planeación agregada se ejecuta en función de los datos con los que trabaja la organización, considerando adicionalmente que la cantidad ideal por lote es de 4000 unidades; esta producción puede ser realizada en cuatro ocasiones en un turno de 8 horas diarias, por lo que mensualmente se podría producir 320.000 unidades. Es importante señalar que la producción de la empresa satisface el 15 % del mercado. Partiendo de estas premisas, es factible elaborar la planeación de la producción considerando diversas posibilidades; inicialmente se encuentra el escenario en el cual se obtiene el costo anual que la empresa obtendría al fabricar el número ideal de unidades determinadas en la programación lineal. Posteriormente, se analizan escenarios en función de la utilización de horas extras, subcontratación de unidades y el costo que obtendría la empresa al buscar ampliar su presencia en el mercado. Al ejecutar la planeación agregada, las variables diseñadas se describen en la tabla 6.

Tabla 6
Variables utilizadas en la planeación agregada

Elaboración propia.

Estas variables permiten plantear la función objetivo, que se describe en la ecuación 8:

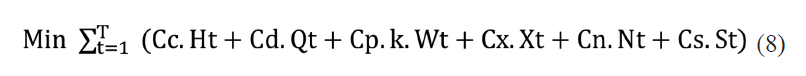
Es importante recordar que la empresa no considera inventarios, razón por la cual dicha variable no es considerada en la planeación agregada propuesta. Las restricciones del modelo vienen determinadas por:

Restricción de fuerza de trabajo

La restricción es aplicada acorde a los requerimientos de los escenarios analizados, en función de las necesidades de ocupar sus variables.

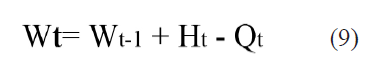
Restricción de niveles de producción

Los niveles de producción están acordes a:

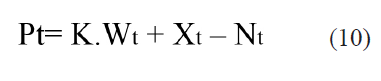
Al aplicar la función objetivo y las restricciones propuestas en el sistema informático Lingo 15.0, los costos alcanzados están en la tabla 7.

Tabla 7
Costos obtenidos (cantidades en dólares)

Elaboración propia.

En la tabla 7, de acuerdo con los resultados encontrados, se evidencia que la metodología de planeación agregada es factible de ser aplicada para la obtención de los costos a partir de los resultados alcanzados por el diseño y resolución del modelo matemático. Los resultados encontrados mediante la aplicación del modelo matemático evidencian resultados futuros muy cercanos a la realidad mediante el desarrollo de un procedimiento lógico y secuencial que guarda coherencia con el planteamiento de las variables, función objetivo y restricciones, reflejando finalmente los resultados económicos a ser alcanzados por la aplicabilidad de esta metodología.

El presente trabajo muestra que la programación lineal es una de las técnicas más útiles de la investigación de operaciones, probando su aplicabilidad en cualquier tipo de empresa, como en el presente caso la industria farmacéutica, y demostrando que es factible encontrar ahorros significativos si esta técnica es aplicada correctamente.