Introducción

Los primeros casos ocurridos por el virus SARS-CoV-2 en China iniciaron la diseminación de la enfermedad coronavirus (COVID-19) por diversos países. El virus se transmitió entre las personas con tanta rapidez que en poco tiempo varios países empezaron a contar casos y a tomar acciones para ralentizar el contagio. En Costa Rica el primer caso por coronavirus se confirmó el 6 de marzo de 2020 (Chaves et al. 2020), proveniente de un vuelo comercial desde Estados Unidos, mientras que para esa fecha en varios países europeos como Italia ya se registraban un acumulado que superaba los 1000 casos, e inclusive estaban contabilizando defunciones asociadas a la COVID-19.

Diversos estudios analizaron datos de distintos países y los resultados han determinado que bajo ciertas circunstancias el comportamiento del crecimiento de casos sigue formas exponenciales y logísticas (Roosa et al. 2020). En la fase inicial de la pandemia en varios países se evidenció un comportamiento esperado según una tendencia exponencial cuando no se adoptaron medidas de mitigación de la transmisión e impacto del contagio, lo cual coincide con los comportamientos exponenciales y subexponenciales esperados en la caracterización inicial de epidemias (Chowell et al. 2016).

La incidencia, o casos nuevos diarios, por el brote de coronavirus es información disponible y reportada por las entidades de salud pública desde la aparición del primer caso en Costa Rica, donde en las primeras etapas de la pandemia se proporcionó información de una manera muy básica mediante infografías y posteriormente mediante plataformas más colaborativas de socialización de información. Sin embargo, en la toma de decisiones para la previsión del impacto del virus se requiere un pronóstico de los casos esperados para días posteriores. El pronóstico toma relevancia para la planificación de acciones de contención que minimicen el impacto tal como la preparación y equipación de los hospitales con las camas y unidades de cuidados intensivos necesarios para dar respuesta al internamiento de pacientes por la COVID-19 (Torabipour et al. 2016).

El modelado estadístico para la proyección de los casos esperados se realizó bajo supuestos que se establecen en función de la complejidad y acción de los modelos. En determinadas situaciones y supuestos se consideraron factores a nivel de modelado que ayudan a seleccionar un modelo que describe en cierta medida el comportamiento actual para poder proyectar a futuros casos.

En Costa Rica, en el estado inicial del contagio la cantidad de casos confirmados fueron pocos, lo cual limitó el uso de modelos epidemiológicos o alguna adaptación que permitiera generar una proyección de casos a partir de información disponible y con supuestos en el contexto de medidas de contención. En general, la cantidad de casos reportados se mantuvo constante y con pocos casos diarios durante los primeros 100 días de la pandemia (CR Ministerio de Salud 2021).

El lento crecimiento de casos provocado por las medidas de contención y la falta de acceso a datos, debido a la confidencialidad de estos, provocaron que los primeros análisis se basaran en modelos que capturaran el comportamiento de los casos acumulados por la COVID-19 y no en el comportamiento diario. También, si se asume que las medidas de contención tenían un efecto en el movimiento del virus, era esperable que el brote en algún momento debía alcanzar un punto máximo o cúspide que reflejaría el control sobre el crecimiento de casos.

La preparación para enfrentar la pandemia alentó al Ministerio de Salud de Costa Rica a acercarse a la Universidad de Costa Rica con la conformación de un equipo de especialistas en diversas disciplinas para la atención de análisis del comportamiento de los casos por coronavirus y el impacto en el uso de camas hospitalarias. El equipo de investigación se conformó con especialistas en gestión de riesgos, estadística, ciencias del comportamiento y procesos de simulación.

El trabajo interdisciplinario del equipo de especialistas permitió valorar el comportamiento de la curva de contagio por la COVID-19 mediante la implementación de las medidas de contención establecidas en el país. En una primera etapa las medidas promovieron el autocuidado mediante el lavado de manos, el distanciamiento físico y la prevención de evitar aglomeraciones, mientras que la segunda etapa se concentró en la reducción de la movilidad en el país mediante la instauración del trabajo remoto de centros escolares, la restricción vehicular, la disminución de la capacidad de espacios públicos y regulación de horarios en las playas, entre otras.

Durante los primeros tres meses de la epidemia el equipo de especialistas realizó al menos cinco informes técnicos que aportaron insumos para la toma de decisiones en el manejo de la epidemia. Los informes incluyeron información de las proyecciones de casos y demanda de camas, así como el comportamiento y análisis del número de reproducibilidad.

Las principales recomendaciones plasmadas en los informes evidenciaron que las intervenciones realizadas por el Ministerio de Salud de Costa Rica modificaron el comportamiento exponencial del contagio a una forma logística, lo cual se reflejó en la capacidad de dar atención a los pacientes con la COVID-19 en las redes hospitalarias. También el equipo de especialistas calculó el número de reproducibilidad en etapas iniciales de la pandemia (Nishiura 2013) demostrando que el valor funcionaba como evidencia de la descripción de la rapidez de la transmisión del virus entre personas.

En la emergencia pandémica es relevante la toma de decisiones basada en evidencia científica y técnica, lo cual significa que la captura de elementos sustentantes de las acciones transforma en retos los estudios y análisis realizados en tiempo real de la emergencia, por lo que es de vital importancia la incorporación, adaptación y calibración de modelos con resultados interpretables y vinculados a la mitigación de contagio (Roosa et al. 2020).

En la emergencia pandémica es relevante la toma de decisiones basada en evidencia científica y técnica, lo cual significa que la captura de elementos sustentantes de las acciones transforma en retos los estudios y análisis realizados en tiempo real de la emergencia, por lo que es de vital importancia la incorporación, adaptación y calibración de modelos con resultados interpretables y vinculados a la mitigación de contagio (Roosa et al. 2020).

Modelos

Modelo de crecimiento exponencial

El modelo exponencial (Paine et al. 2012) corresponde al conformado por dos parámetros, los cuales permiten establecer el comportamiento de los datos de los casos acumulados. El modelo captura el comportamiento en dos fases: en una primera fase los datos diarios crecen en función de un valor inicial y en una segunda etapa se acelera el crecimiento de casos. La expresión del modelo exponencial se describe como

donde t representa el consecutivo de días y y es la variable dependiente que representa la cantidad de casos acumulados y los parámetros a y b describen el comportamiento inicial y la rapidez del crecimiento, respectivamente. Otra versión del modelo exponencial que incluye un parámetro adicional se expresa como

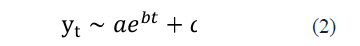
donde c corresponde a la intersección con el eje de las ordenadas.

Modelo de crecimiento logístico

El modelo logístico (Paine et al. 2012) se conforma de tres parámetros que permiten establecer el comportamiento de los datos en tres fases: en una primera fase los datos diarios crecen de forma lenta, en una segunda etapa se acelera el crecimiento de casos para luego entrar en la tercera fase donde se alcanza la capacidad de carga del modelo con un comportamiento asintótico. La expresión del modelo logístico se describe como

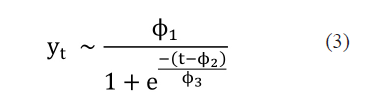
donde los parámetros ϕ1, ϕ2 y ϕ3 describen el comportamiento de capacidad de carga, simetría del comportamiento y la rapidez del crecimiento, respectivamente.

Modelo de Richards

El modelo de Richards (Tjørve y Tjørve 2010) permite observar el comportamiento subexponencial y la potencial transición desde el comportamiento logístico al exponencial. El modelo de Richards se expresa como

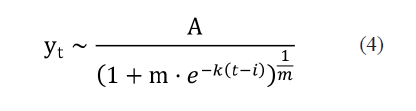
donde los cuatro parámetros describen la asíntota superior A , el mínimo o asíntota inferior k, el factor de crecimiento m, y el máximo relativo del factor de crecimiento i. El modelo de Richards subsume otros modelos como el modelo de crecimiento logístico y el de Gompertz. Si i = 1, se obtiene el modelo logístico y cuando m = s se deriva el modelo de Gompertz (Oswald et al. 2012).

Método

Supuestos

Los análisis que se realicen con los modelos previamente mencionados asumen que el comportamiento del crecimiento de casos se da a partir de los siguientes supuestos:

1. Hay al menos una persona contagiada en la población.
2. Las personas contagiadas y no contagiadas tienen contacto entre ellas.
3. Hay una cantidad de personas sin contagio que potencialmente se contagiarán.
4. Las medidas sanitarias permiten el control del contagio por lo que se tendrá un máximo de contagios menor que la población susceptible.
5. Las personas que hayan estado en contacto con las personas contagiadas deben identificarse rápidamente.
6. El crecimiento exponencial y las medidas sanitarias compiten entre sí.

Datos

Los datos corresponden a los casos confirmados desde el 6 de marzo al 6 de junio de 2020 por contagio de la COVID-19 en Costa Rica. Los datos han sido registrados a partir de los reportes diarios emitidos por el Ministerio de Salud, tanto vía conferencia de prensa en formatos de imagen y más recientemente en formatos de hojas de cálculo que facilitan la transferencia de la información.

Estimación de modelos

Se realizó la estimación de cuatro modelos con el método de mínimos cuadrados no lineales: logístico, exponencial, Richards y Gompertz. Los modelos se estiman con los algoritmos de mínimos cuadrados (Florent et al. 2015) implementados en la plataforma de R en la paquetería FlexParamCurve (Oswald et al. 2012). Dado que los modelos requieren valores iniciales para la estimación, se utilizó las funciones self-starting, las cuales permiten el proceso de arranque en la estimación de los parámetros. A partir de los parámetros estimados, se generaron los pronósticos, los intervalos de confianza y los de predicción de las estimaciones, los cuales se calculan a partir de la expansión de Taylor de primer y segundo orden y simulación Montecarlo implementados en la librería propagate (Spiess 2018).

Simulación de demanda de camas hospitalarias

Los valores de casos acumulados proyectados se incorporaron a un modelo de simulación aleatoria de eventos discretos que generó la demanda de camas hospitalarias. En el modelo los incrementos y los decesos de casos no generaron el alcance de un estado estacionario tal como ocurre en el modelado de procesos de servicios o de producción. El código de generación de las camas requeridas según la proyección se implementó en lenguaje Python.

A partir de estudios preliminares en Italia de Grasselli, Pesenti y Ceconi (2020) y Livingston y Bucher (2020) se consideró que en la proyección de uso de camas el 80 % de las personas contagiadas por la COVID-19 no requerían hospitalización, el 15 % de los infectados pasaban a una cama de atención general y el 5 % requería una cama o unidad de cuidados intensivos (UCI). Además, se estableció una estadía promedio de 6 días (desviación estándar de 3,6) para las personas que requieren atención general y un tiempo promedio de 11 días (desviación estándar de 6,5) para la estancia en unidad de cuidados intensivos (UCI).

El algoritmo inicia generando una cantidad de pacientes según una distribución normal estándar e incorpora la cantidad de casos proyectados diariamente. Luego, a cada paciente se le genera un día de hospitalización y se le asigna una de las tres rutas según la probabilidad de la necesidad de atención en cama general, cuidados intensivos o por no requerir hospitalización. Finalmente, se obtiene el número de camas requeridas en función de la cantidad contagios pronosticados. El proceso es iterativo y se repite 1000 veces para calcular el promedio y la desviación estándar de la cantidad de camas requeridas. La cantidad alta de réplicas compensaron la limitada cantidad de días de pronóstico disponible.

Estimación del número de reproducibilidad

La estimación de los pronósticos se acompañó de un análisis de la tasa de reproducibilidad, R_t con dependencia en el tiempo (Cori et al. 2013). El número de reproducibilidad indica la cantidad de personas que se contagian a partir de una persona infectada (Nishiura 2013). La tasa permite observar, a nivel general, si las medidas de contención han producido algún cambio en el comportamiento de la transmisión del virus puesto que el R_t se calcula posterior a que se hayan adoptado medidas de contención.

Los valores del R_t superiores a 1 indican que el comportamiento es acelerado y los valores por debajo de 1 representan que el contagio empieza a desacelerarse. El R_t se calculó con estimación bayesiana con rezagos de 7 días que siguen una distribución gamma. El análisis se implementó en el programa R con la librería EpiEstim (Cori et al. 2020).

Conformación de un equipo de especialistas

El Ministerio de Salud de Costa Rica solicitó a la Universidad de Costa Rica la conformación de un equipo de especialistas en diversas disciplinas para la atención de análisis del comportamiento de los casos por coronavirus y el impacto en el uso de camas hospitalarias. El equipo de investigadores se conformó con especialistas en gestión de riesgos, estadística, ciencias del comportamiento y procesos de simulación.

El equipo realizó al menos 5 informes técnicos que aportaron insumos para la toma de decisiones en el manejo de la epidemia. Los tres primeros informes, con información de las proyecciones y demanda de camas, se realizaron el 8, 14 y 23 de abril de 2020, mientras que el cuarto reporte del 10 de mayo de 2020 presentó el comportamiento y análisis del número de reproducibilidad. Finalmente, el quinto informe se dio el 5 de junio de 2020 con un análisis por semanas del índice de transmisibilidad.

Resultados

Los resultados se muestran en tres vertientes. En la primera se presentan los parámetros estimados a partir de los modelos y resultados de predicción a partir de los distintos modelos. Posteriormente, se muestran los pronósticos de las demandas de camas hospitalarias. Seguidamente, se describe el comportamiento del número de reproducibilidad. Finalmente, se muestra la optimización de los modelos y simulaciones para la toma de decisiones.

La figura 1 muestra el análisis con los datos de los primeros 17 días con el modelo exponencial, el cual evidencia la posible tendencia que tomaría el comportamiento del coronavirus en Costa Rica. Según se aprecia en la figura 1, en los primeros 10 días se marcó una tendencia exponencial: sin embargo, con la declaratoria del estado de emergencia nacional y de confinamiento a partir del día 11, la tendencia de casos reales se alejó de la forma exponencial, lo cual sugirió un potencial efecto de las medidas sanitarias y por ende la presencia de un comportamiento logístico. Este hecho se observa en la curva de casos diarios observados, la cual presenta un crecimiento hasta el día 22 o 23 y luego decrece hasta el día 50.

Los resultados desplegados en la figura 1 marcaron el camino para realizar el modelado subsecuente con los cuatro modelos. La tabla 1 muestra los parámetros estimados a partir de los modelos. Los resultados se presentan en escenarios que permiten valorar comportamiento de los datos. El escenario pesimista está estipulado por un crecimiento acelerado bajo el modelo exponencial y el escenario optimista está representado por el modelo logístico donde se asume que hay un control sobre el ritmo de aparición de casos. En el medio de los escenarios optimista y pesimista se encuentran los modelos que marcan una potencial transición entre los escenarios. Los escenarios intermedios están representados con los modelos de Richards y Gompertz.

Los parámetros estimados en la tabla 1 permiten observar que los valores obtenidos con la serie de datos de 1-34 plantearon un punto de inflexión entre el día 22 y 23. Este punto de inflexión denota un primer pico de casos que marca la tendencia de la primera ola del brote. El valor de la asíntota horizontal para los datos 1-34 evidenció que la capacidad máxima de casos acumulados estaría alrededor de los 668 con el modelo de Gompertz. Los casos observados acumulados rondaron los 700 al momento en que la primera ola terminó su caída entre los días 49 a 56.

Figura 1
Panel superior: estimación del modelo exponencial
para los casos acumulados en los primeros 17 días de epidemia.
Panel inferior: curva de casos diarios observados

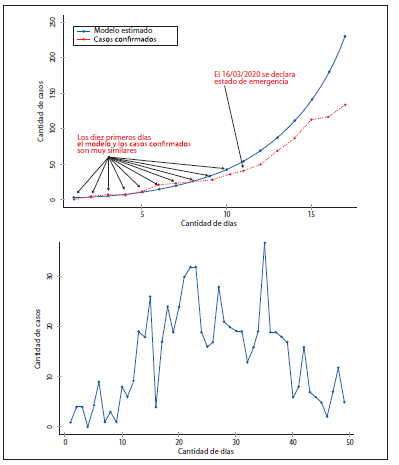
Elaboración propia.

Los valores del parámetro de crecimiento en el modelo exponencial tendieron a disminuir desde 0,08 a 0,05 conforme se fueron utilizando más datos en los modelos. Este comportamiento del modelo exponencial se corresponde con la desaceleración de la aparición de casos después del día 23 del inicio de la pandemia.

Tabla 1
Parámetros de los estimados en tres distintos momentos

Elaboración propia.

La figura 2 muestra la transición potencial desde un escenario con comportamiento logístico (línea azul) hasta un escenario con comportamiento exponencial (línea negra) y dos escenarios intermedios a partir de la serie de datos observados desde el día 1 al día 34. El crecimiento de casos diarios sigue un comportamiento con forma sigmoide desde el día 1 hasta el 49, ubicándose ya sea sobre la curva logística o la de Gompertz. En el panel inferior de la figura 3 las curvas de Gompertz y Richards coinciden en el pronóstico de los casos.

Al día 34, el crecimiento de los datos se ubica sobre el escenario intermedio representado por la curva de Gompertz, mientras que al día 40 los casos acumulados se mantuvieron sobre la curva de Richards y al día 49 retomó la forma de Gompertz. El mantenimiento de la forma sigmoide es un indicativo de que las medidas adoptadas por el Ministerio de Salud mantuvieron cierto control en el crecimiento de los casos.

Figura 2
Proyección de casos acumulados según cuatro modelos:
exponencial, Gompertz, Richards y logístico. Panel izquierdo:
datos 1-34 días. Panel derecho: datos 1-49 días

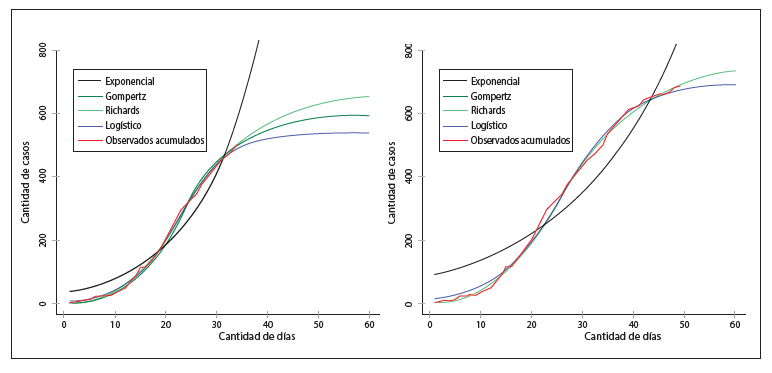
Elaboración propia.

La tabla 2 muestra los valores de la demanda de camas pronosticadas según los escenarios de análisis y tipos de camas. La ocupación real de las camas de cuidados intensivos no superó los 14 días en el período de los primeros tres meses de la pandemia. La cantidad de camas de cuidados intensivos proyectadas tendió a disminuir conforme se avanzó en el tiempo puesto que conforme se emplearon más datos de la serie de casos reportados se requirió una mayor cantidad de días para alcanzar la demanda máxima de camas.

En concordancia con el comportamiento de los casos con las curvas logística o Gompertz, se observa que las camas UCI proyectadas con la serie de días 1-34 permitió pronosticar el comportamiento real de las camas UCI. El modelo logístico estableció la necesidad máxima de 17 camas en 10 días, mientras que la estimación en el escenario Gompertz fue de 23 camas en 19 días.

Tabla 2
Pronóstico de camas requeridas según tipo de cama

Elaboración propia.

La figura 3 muestra la estimación del número de reproducibilidad según hitos relevantes en el período del 1-40. El comportamiento del índice durante los primeros tres meses evidenció que las medidas adoptadas en los primeros 20 días de la epidemia tuvieron control sobre el crecimiento de casos. Al inicio de la epidemia el Rt tomó valores bastante altos alrededor de 3,5 reflejando la rapidez con la que se movía el virus entre el caso primario y los casos secundarios, sin embargo, con el paso de los días el valor tendió a estabilizarse y descendió a valores cercanos a 1.

Figura 3
Número de reproducibilidad con dependencia en el tiempo

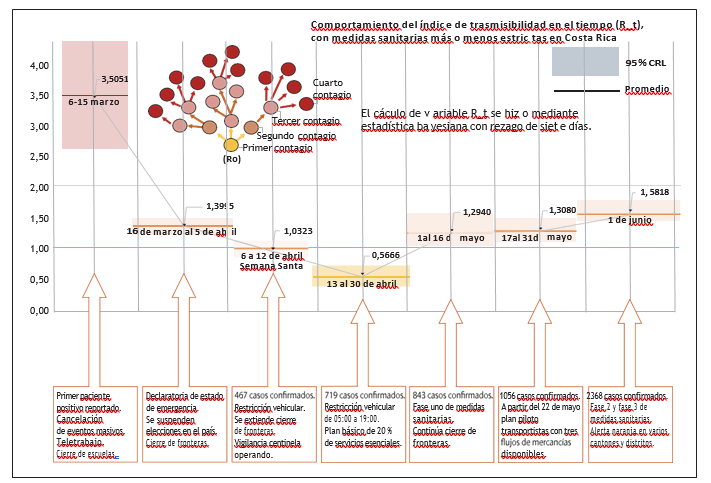
Elaboración propia.

El equipo de investigación generó como complemento a los modelos de aproximación y simulación en la primera etapa del análisis de los datos antes descritos, la optimización por medio de informes técnicos la forma de presentar gráficos y los análisis para interpretación menos compleja y de mayor facilidad de acceso para los tomadores de decisiones. Esto con el objetivo de aplicar métodos de decisión optimizados, lo cual permite contar con un proceso sistemático, consistente y conciso, que faculte una toma decisiones lo más efectiva posible.

La figura 4 muestra un ejemplo de la optimización de la información mediante gráficos. El gráfico de la figura 4 presenta un panel de termómetro que representa los límites de los distintos niveles de alerta según la cantidad de casos diarios, semanales y ocupación de camas. Por ejemplo, durante los primeros tres meses una cantidad de casos superior a 33 y una ocupación de camas mayor a 70 marcó la caracterización en un nivel 3 de alerta.

Figura 4
Ejemplo de gráfico optimizado de resultados de simulación
de camas UCI para toma de decisiones de autoridades sanitarias

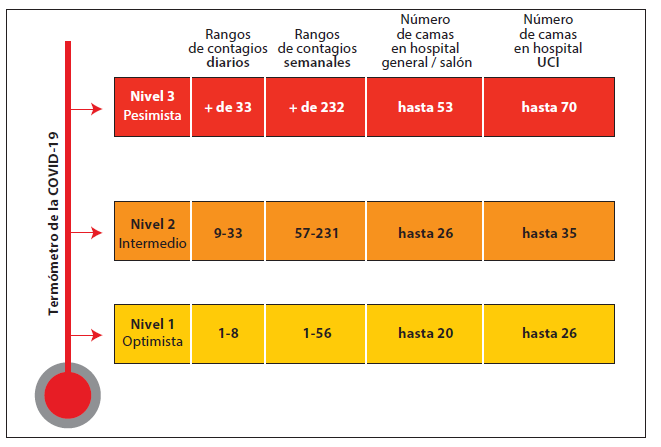
Elaboración propia.