Sergio Torrico-Salamanca

Universidad Privada Boliviana. La Paz, Bolivia sergioedwintorricosalamanca@gmail.com.
Resumen
La crisis financiera mundial, iniciada en 2007, ha marcado un antes y un después en la administración de riesgos contemporánea, no desde el punto de vista del desarrollo de la administración de riesgos, sino desde la necesidad de aplicar lo desarrollado y utilizarlo oportunamente, tanto por parte de las instituciones financieras como por los reguladores y el Estado. De acuerdo con Dionne (2013), el estudio de la administración de riesgos se ha desarrollado desde la finalización de la Segunda Guerra Mundial, por lo que ha tenido más de 50 años para evolucionar con relación a técnicas cuantitativas y científicas. Este artículo propone el uso de paneles dinámicos para la cuantificación agregada del riesgo de crédito, utilizando la metodología de Macro Credit Scoring; se construye un modelo econométrico para medir el riesgo de crédito de un sistema bancario en función del crecimiento económico y del perfil financiero de los bancos (que refleja su perfil de riesgo). Para la metodología se utilizó lo propuesto por Arellano-Bond para controlar la endogeneidad entre el riesgo de crédito y el crecimiento económico; se estima la medida de pérdida esperada como producto final. Se determinó que la cobertura por riesgo de crédito es adecuada en Bolivia y se demuestra la aplicabilidad de la metodología propuesta.
Palabras clave: riesgo de crédito, gestión cuantitativa de riesgos, banca, paneles dinámicos, pérdida esperada.
JEL: G32 Riesgo financiero y gestión de riesgos.
Abstract
The global financial crisis that began in 2007, has marked a before and after in contemporary risk management, not from the point of view of developing risk management, but from the need to apply what has been developed, and to use it in a timely manner both by financial institutions as well as by regulators and the State. According to Dionne (2013), the study of risk management has been developed since the end of the Second World War, so it has had more than 50 years to evolve in relation to quantitative and scientific techniques. This article proposes the use of dynamic panels for the aggregate quantification of credit risk, using the Macro Credit Scoring methodology; an econometric model is built to measure the credit risk of a banking system based on economic growth and the financial profile of banks (which reflects their risk profile). For the methodology, what Arellano-Bond proposed was used to control the endogeneity between credit risk and economic growth, estimating the expected loss measure as a final product. It was determined that the credit risk coverage is adequate in Bolivia and the applicability of the proposed methodology is demonstrated.
Key words: Credit risk, quantitative risk management, banking, dynamic panels, expected loss.
JEL: G32 Financial risk and risk management.
Resumo
A crise financeira mundial iniciada em 2007 foi um divisor de águas na administração de riscos contemporânea, não do ponto de vista do desenvolvimento da gestão de riscos, mas desde a necessidade de se aplicar o desenvolvimento e utilizá-lo oportunamente tanto por parte das instituições financeiras como por parte dos reguladores e do Estado. De acordo com Dionne (2013), o estudo da administração de riscos se desenvolveu a partir do fim da Segunda Guerra Mundial e teve, portanto, mais de 50 anos para evoluir em relação a técnicas quantitativas e científicas. Este artigo propõe o uso de painéis dinâmicos para a quantificação agregada do risco de crédito por meio da utilização da metodologia de Macro Credit Scoring, construindo-se um modelo econométrico para medir o risco de crédito de um sistema bancário em função do crescimento econômico e do perfil financeiro dos bancos (que reflita seu perfil de risco). Como metodologia, utilizou-se a proposta de Arellano-Bond para controlar a endogeneidade entre o risco de crédito e o crescimento econômico, estimando-se a medida de perda esperada como produto final. Determinou-se que a cobertura por risco de crédito é adequada na Bolívia, demonstrando-se a aplicabilidade da metodologia proposta.
Palavras-chave: Risco de crédito, gestão quantitativa de riscos, banco, painéis dinâmicos, perda esperada.
JEL: G32 Risco financeiro e gestão de riscos.
Introducción
Este artículo se enmarca en la administración de riesgos, específicamente en el riesgo de crédito y su medición mediante la determinación de la pérdida esperada utilizando la técnica de paneles dinámicos; se propone la aplicación de la metodología de Macro Credit Scoring, modelando una variable continua en lugar de una variable discreta para la cartera de créditos agregada de bancos. Para este fin, la metodología propuesta implica la modelización del riesgo de crédito basada variables que reflejan el perfil financiero de los bancos y variables macroeconómicas.
Mediante esta aplicación se muestra cómo se puede incluir el impacto macroeconómico en la determinación del riesgo de crédito y, por otro lado, se obtiene evidencia empírica sobre la relación de variables macroeconómicas y de perfil financiero de los bancos sobre la medición del riesgo de crédito.
Esta es una investigación cuantitativa. La población analizada son los bancos del Sistema Bancario Comercial de Bolivia (en adelante, SBCB) y se desarrolla el análisis mediante el uso de paneles dinámicos.
Se desarrollan los siguientes objetivos:
- Proponer una herramienta de medición del riesgo de crédito para la determinación de la pérdida esperada en un sistema bancario comercial mediante el diseño y adaptación de técnicas de medición existentes.
- Cuantificar el riesgo de crédito mediante la medida de pérdida esperada en el SBCB.
- La medición de riesgo de crédito para pérdidas esperadas es aplicable en un sistema bancario comercial consolidado mediante la técnica de Macro Credit Scoring.
- La medida de pérdida esperada del SBCB es adecuada respecto a su riesgo.
Las hipótesis planteadas son:
A continuación, se presenta el mapa del artículo; primero se muestra una revisión breve de la literatura, luego se presenta la descripción de la metodología propuesta, para finalmente mostrar la aplicación de la metodología propuesta a un caso práctico en el SBCB.
Marco teórico
En la literatura, el Credit Scoring se enfoca principalmente en el desarrollo de modelos empíricos para la toma de decisiones en la industria de los créditos masivos, también conocidos como retail (Crook, Edelman y Thomas 2007), en donde el objetivo se centra en la obtención de una probabilidad, basada en un modelo, sobre un posible comportamiento no deseado de un cliente crediticio en el futuro (Lessman et al. 2015).
Al ser una herramienta basada en modelos, depende de la metodología cuantitativa que se utiliza para mejorar la precisión, por lo que Lessman et al. (2015), en un estudio reciente, orientado al benchmarking del estado del arte de los algoritmos de clasificación para Credit Scoring, concluyen que la literatura no refleja los avances recientes en la capacidad de predicción de los modelos.
Entre otros resultados, dicho estudio incluye, de forma comparativa al método de clasificación sencillo (o LR, por sus siglas en inglés), y los datos arrojados por el estudio muestran que si bien no es la técnica que muestra un mejor desempeño, está por encima de la media, y es acorde a lo propuesto por Finlay (2009), quien presenta evidencia sobre los algoritmos complejos de clasificación, mismos que no ofrecen mucha ventaja sobre el uso de métodos más simples.
Este documento y la propuesta del Macro Credit Scoring no está enfocado en proponer mejoras metodológicas a la clasificación de algoritmos.
Las variantes al uso tradicional del Credit Scoring son: i) no se propone para clasificar clientes, sino para clasificar la cartera agregada de clientes perteneciente a un banco; ii) al trabajar con datos agregados, las variables explicativas también son agregadas (macro).
La normativa prudencial emitida por el Comité de Basilea en Supervisión Bancaria (CBSB, por sus siglas) ha sido orientada, durante casi 10 años, a mejorar las metodologías de cuantificación de riesgo de crédito, especialmente mediante las reformas implementadas luego de la crisis financiera mundial iniciada en 2007 con la crisis de las hipotecas subprime en Estados Unidos, aspecto que se puede observar en el estudio “Basilea III: finalizando las reformas poscrisis” (CBSB 2017); sin embargo, estas metodologías están enfocadas principalmente en la gestión bancaria interna, y no así en su aplicación a nivel macroprudencial, en especial para sistemas bancarios comerciales.
Entre más de 120 documentos publicados durante el período 2015-2017 por el Banco de Pagos Internacionales (BIS Papers), solo se identificaron 12 artículos que abordan temas directamente relacionados al crédito y su riesgo. A continuación, se detallan los papers. Ayyagari y Beck (2017) y Park (2007) analizan la relación entre el crecimiento del crédito y las políticas macroprudenciales; Soh, Chong y Chuah (2017) y Deng (2017) examinan el crédito del hogar, crecimiento y desigualdad en Malasia; McGuire y Ehlers (2017) y Hoggarth (2017) estudian a los bancos extranjeros y las condiciones de créditos en economías de mercados emergentes; Schularick y Shim (2017) y Choi (2017) observan el crédito del hogar en la región de Asia-Pacífico; Ravalo (2017) evalúa si se tiene suficiente información para calibrar una intervención adecuada analizando la acumulación de crédito y problemas de estabilidad financiera; Fendoğlu (2016) revisa los ciclos del crédito y el marco de política macroprudencial en países emergentes; Başkaya et al. (2017) detallan la relación entre las políticas macroprudenciales, los flujos de capital y los ciclos de crédito; y, finalmente, Santos (2017) recoge las implicaciones de los booms crediticios para los sectores público y privado.
Autores como Belloti y Crook (2009) testean el uso de variables macroeconómicas en la técnica tradicional del Credit Scoring con resultados positivos, ya que la inclusión de este tipo de variables brinda una mejora estadística significativa en la predicción de los modelos. Por otro lado, Rocha, Joao y Brandao (2013) analizan el impacto de la inclusión de factores económicos en modelos de Credit Scoring con resultados también positivos, anticipando que este tipo de estudio puede ser extendido a otras aplicaciones de riesgo con éxito.
Tomas (2010) resalta la necesidad de incluir factores económicos y condiciones de mercado en los sistemas actuales de gestión del riesgo, en particular con el riesgo crediticio en la industria de créditos masivos, trabajado desde los modelos de Credit Scoring.
Las variables que se incluyen están relacionadas a tasas de interés, ingresos, índice de mercado, desempleo, producción, precios inmobiliarios, confianza del consumidor, consumo privado, inflación, salarios, gasto de hogares e impuestos.
De Guimarães e Souza y Feijó (2011) encontraron, a partir de un estudio realizado para el sistema bancario de Brasil, que existe una relación entre las variables macroeconómicas y el riesgo crediticio de los bancos, y proponen que la interacción de la macroeconomía y los bancos debe ser considerada al momento de tomar decisiones de política económica.
La tabla 1 sistematiza los estudios que se concentran en la influencia de las variables macroeconómicas sobre el riesgo de crédito.
Tabla 1
Influencia: variables macroeconómicas
sobre riesgo crediticio
| Estudio | Ámbito geográfico analizado | Variables identificadas |
|---|---|---|
| Aver (2008) | Portafolio de créditos del sistema de Eslovenia. | Empleo / desempleo, tasas de interés, valor del mercado de valores. |
| Kattai (2010) | Sistema bancario de Estonia, Letonia, Lituania. | Crecimiento, tasas de interés. |
| Salas y Saurina (2002) | Sistema bancario de España. | |
| Jakubík (2007) | Sistema bancario de la República Checa. | |
| Bohachova (2008) | Bancos en países de la Organización para la Cooperación y el Desarrollo Económicos (OCDE) y países que no se pertenecen a la OCDE. | Ciclo económico. |
| Nkusu (2011) | Países de economías avanzadas. | Desarrollo económico. |
Elaboración propia.
El término Macro Credit Scoring ha sido propuesto por el autor, Torrico (2014), en un planteamiento previo que modelaba el riesgo de crédito con la construcción de una variable binaria (discreta) y con una metodología que imponía el supuesto de exogeneidad entre las variables riesgo de crédito e ingreso; esa primera exploración sirvió de base para ampliar el análisis y explorar herramientas más sofisticadas que permitan potenciar la capacidad de medición de esta metodología.
Metodología
En esta sección se presenta la metodología de Macro Credit Scoring, así como el esquema propuesto (tabla 2) para la explotación del Credit Scoring.
En la tabla 2 se propone calcular la probabilidad de incumplimiento de la cartera de créditos de un banco de forma agregada, con el fin de cuantificar el riesgo de crédito que tiene el banco en su cartera, de este modo esta metodología se enfoca en la probabilidad de incumplimiento (PD) pero mediante una adaptación innovativa:
E[L] = PD × LGD × EAD (1)
Donde:
EL = pérdida esperada.
PD = probabilidad de incumplimiento.
EAD = exposición al incumplimiento.
LGD = pérdida dado el incumplimiento.
Luego, se puede reordenar (1) para expresar la pérdida esperada como porcentaje de la exposición (ajustada por la pérdida dado el incumplimiento) para mostrar una probabilidad de incumplimiento agregada.
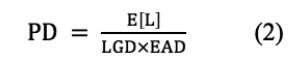
Cabe resaltar que no se está buscando medir la probabilidad de incumplimiento del banco como tal, ya que para ese fin simplemente se estaría aplicando la técnica del scoring a individuos de una industria como cualquier
Tabla 2
Macro Credit Scoring como metodología para la cuantificación
del riesgo de crédito agregado
| Procedimiento actual | |||
|---|---|---|---|
| Entidad 1 | Cliente 1,1 |  |
Probabilidad de incumplimiento cliente 1,1 = f (características asociadas al cliente 1,1; variables de control). |
| ... |  |
... | |
| Total 1 |  |
Agregación probabilidad de incumplimiento clientes banco 1. | |
| ... | |||
| Entidad n | Cliente 1,n |  |
Probabilidad de incumplimiento cliente 1, n = f (características asociadas al cliente 1, n; variables de control). |
| ... |  |
... | |
| Total n |  |
Agregación probabilidad de incumplimiento clientes banco n. | |
 |
|||
| Procedimiento propuesto | |||
| Entidad 1 | Cartera consolidada de créditos de clientes 1,1 al n,1 |  |
Probabilidad de incumplimiento cartera entidad 1 = f (características asociadas a la entidad 1; variables macroeconómicas; variables de control [perfil de riesgo]). |
| ... | |||
| Entidad n | Cartera consolidada de créditos de clientes 1,n al n,n |  |
Probabilidad de incumplimiento cartera entidad n = f (características asociadas a la entidad n; variables macroeconómicas; variables de control [perfil de riesgo]). |
| Sistema |  |
Agregación probabilidad de incumplimiento entidad 1 a la entidad n. | |
Fuente: adaptado de Crook, Edelman y Thomas (2007). Tabla simplificada sobre la base de Torrico (2014). Elaboración propia.
otra, como es el caso del estudio de Gurný y Gurný (2013), donde se intenta predecir la quiebra de bancos y no se analiza la cartera que tiene el banco. En este caso se busca medir la probabilidad de incumplimiento de la cartera del banco, en base a su perfil financiero (que refleja su perfil de riesgo) y el comportamiento de variables económicas.
Existe una gran variedad de metodologías alternativas propuestas para medir el riesgo de crédito de bancos y sistemas bancarios de forma agregada. Por ejemplo, Pak-wing y Wong (2008) aplican un modelo VAR, técnica que es también utilizada para tests de estrés sobre bancos (stress testing); Wickens (2011) aplica la técnica de los modelos de equilibrio general dinámico y estocástico (DSGE, por sus siglas en inglés) de bancos e intermediación financiera en el que puede cuantificar el riesgo de incumplimiento; y, Chen y Shia (2011) evalúan la técnica de simulación en la administración del riesgo de crédito para instituciones bancarias.
Ventajas y desventajas de la metodología propuesta
La principal ventaja es la disponibilidad de información; las instituciones financieras no pueden acceder a información de clientes de otras instituciones financieras por un tema de competencia, mientras que la información agregada de las carteras de los bancos es pública en el ámbito mundial en los sistemas bancarios y, por tanto, es más factible trabajar con ella para cuantificar el riesgo de crédito en un sistema bancario o de los bancos que lo componen.
Por otro lado, entre las desventajas de la metodología se puede mencionar que los resultados obtenidos dependen de los supuestos que se manejen durante el diseño de las variables y en el uso de técnicas paramétricas; al agregar la información, como en cualquier análisis macro o agregado, no se determina el comportamiento de determinados segmentos demográficos o poblacionales al interior de la muestra. Como ejemplo se puede mencionar el estudio sobre crecimiento económico de Acemoglu, Johnson y Robinson (2005), quienes estudian la relación entre crecimiento e instituciones, y la investigación de Esfahani y Ramírez (2003), quienes indagan la relación entre la infraestructura y el crecimiento económico; en general, estos estudios delimitan el análisis a indicadores de crecimiento agregado o macro, cuando se podría analizar el crecimiento por sector, por componente del gasto, por región, o por otras segmentaciones.
Un problema habitual, atribuido a los modelos de Credit Scoring, es el sesgo de selección en el sentido descrito por Heckman (1979), ya que la información se limita a la cartera otorgada dado un exitoso proceso de otorgación según explica Greene (1998), por lo que la información disponible no contempla solicitudes rechazadas.
Aplicación de la metodología propuesta
En esta sección se aplica al SBCB la metodología propuesta con el fin de cuantificar la probabilidad de incumplimiento de las carteras de crédito de los bancos como medida del riesgo de crédito.
Análisis de los datos
La base de datos utilizada para el análisis del presente artículo se compone de 877 observaciones en una estructura de datos de panel de 19 bancos, en el intervalo de marzo de 2005 a junio de 2017, con una periodicidad trimestral. Esta es la información de 12 años de todos los bancos del SBCB, basada en series históricas construidas a partir de las publicaciones del ente regulador que es la Autoridad de Supervisión del Sistema Financiero (ASFI).
Variable dependiente
La variable dependiente es continua y utilizada para modelar la probabilidad de incumplimiento de la cartera de las entidades analizadas, donde:
Cartera vencida + cartera en ejecución + cartera vigente = cartera bruta, la tasa de incumplimiento estará dada por (cartera vencida + cartera en ejecución) / cartera bruta.
A continuación, en los gráficos 1-A y 1-B se presenta la evolución de la variable dependiente en el período de análisis:
Gráfico 1-A
Evolución de la tasa de incumplimiento
de las entidades del SBCB*
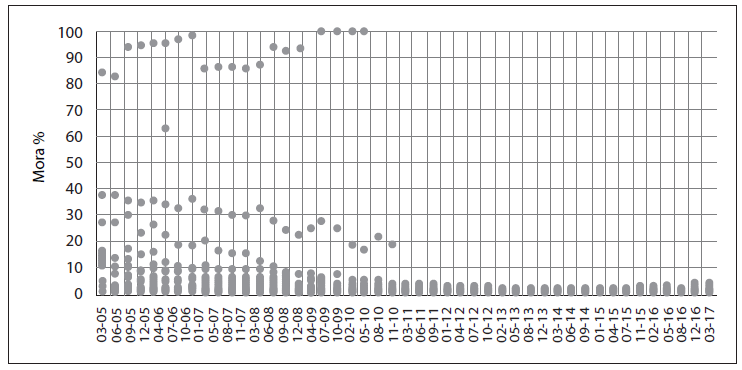
* Evolución: de 5 de marzo a 17 de junio de 2020.
Fuente: información de ASFI (Bolivia).
Fráfico 1-B
Evolución de la tasa de incumplimiento
de las entidades del SBCB*
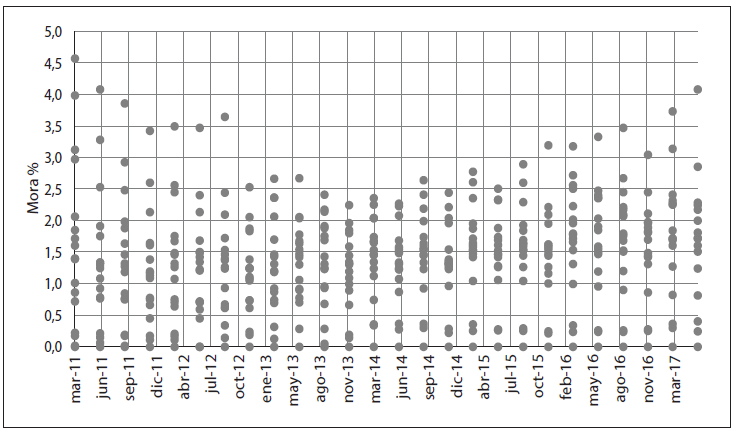
* Evolución: de 5 de marzo de 2011 a 17 de junio de 2017.
Fuente: información de ASFI (Bolivia).
En el gráfico 1-A se muestra la evolución trimestral del ratio de mora de las 19 entidades que componen el sistema analizado. Se muestran los gráficos 1-A y 1-B de forma conjunta, ya que debido a la existencia de datos de entidades en proceso de cierre hasta junio de 2010 se tienen tasas de mora atípicas (de hasta 100 % en el gráfico 1-A), que disminuyen la visibilidad de la varianza de la mora entre entidades. Para una mejor visualización de la varianza de la mora entre entidades, se muestra un acercamiento del gráfico para el período marzo de 2011 hasta junio de 2017.
Uno de los hallazgos es que durante el período de análisis se tiene una tendencia de mejora de la mora de la cartera en el sistema (tendencia decreciente) y que la varianza de la mora se reduce mientras la mora se reduce.
Variables independientes
Se analizan de forma teórica y empírica las variables identificadas como representativas, teórica a partir de la propuesta de Berger y De Young (1997), que utilizan ratios de las instituciones, y empírica porque no se utilizan las mismas variables.
Entre las variables independientes disponibles se cuenta con el grupo de ratios financieros que muestran el perfil financiero de las entidades, y sobre la base de lo propuesto también muestran una aproximación del perfil de riesgo de estas. Por otro lado, se tiene un conjunto de variables macroeconómicas que afectan al desempeño de las carteras de las instituciones bancarias.
Se presenta el análisis completo de las variables que han resultado significativas en el período analizado.
Tabla 3
Variables independientes que han resultado significativas
| Definición | Variable independiente |
|---|---|
| Crecimiento económico | Variación interanual PIB trimestral (c1). |
| Estructura activos | Disponibilidades / activos (x1). |
| Liquidez | (Disponib.+ inv. temp.) / oblig. a corto plazo (x39). |
Elaboración propia.
Son dos variables explicativas financieras y una variable explicativa macroeconómica. Entre estas se tiene la estructura de activos, nivel de liquidez, que representan adecuadamente el perfil de riesgos de una entidad, y sobre la base de lo propuesto en este estudio también dan una muestra del perfil de riesgo que tiene.
En el caso de las variables económicas, se incluye la variable que representa el crecimiento económico, utilizando la variación interanual del PIB trimestral de Bolivia.
A continuación, se presentan los gráficos de las variables independientes utilizadas.
La primera variable analizada es el ratio de disponibilidades/activos:
Gráfico 2-A
Variable (disponibilidades/activos) %
para las 19 entidades del SBCB*
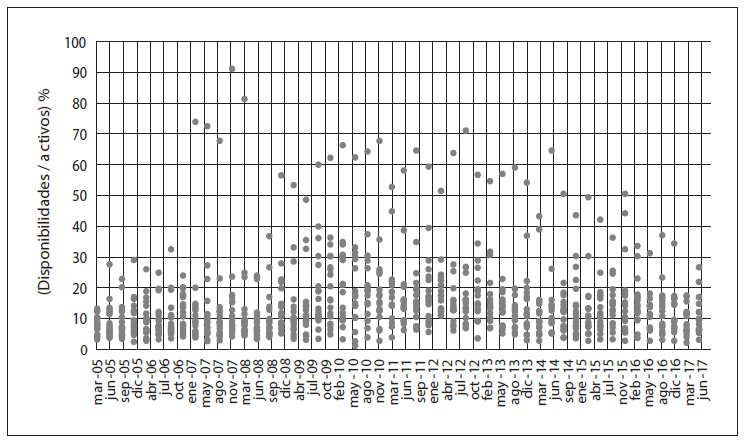
* Evolución: de 5 de marzo a 17 de junio.
Fuente: información de ASFI (Bolivia).
Gráfico 2-B
Variable (disponibilidades / activos) % para las 19 entidades del SBCB*
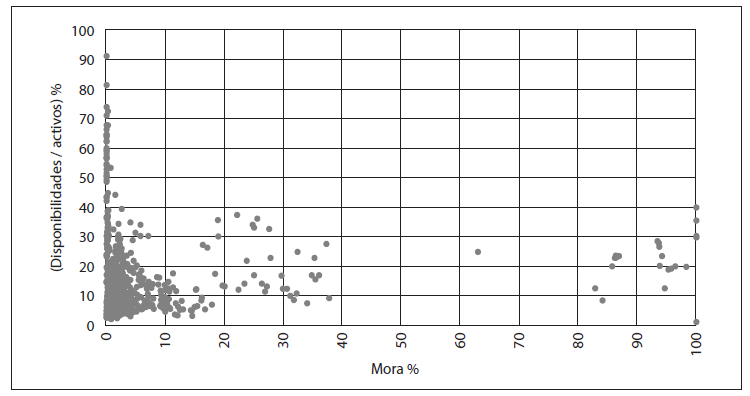
* Dispersión comparativa con la variable mora %. Evolución: de 5 de marzo a 17 de junio.
Fuente: información de ASFI (Bolivia).
A continuación, se presenta una variación del ratio que incluye a las inversiones temporarias:
Gráfico 3-A
Variable ([disponibilidades + Inversiones temporarias] / obligaciones a corto plazo)
% para las 19 entidades del SBCB*
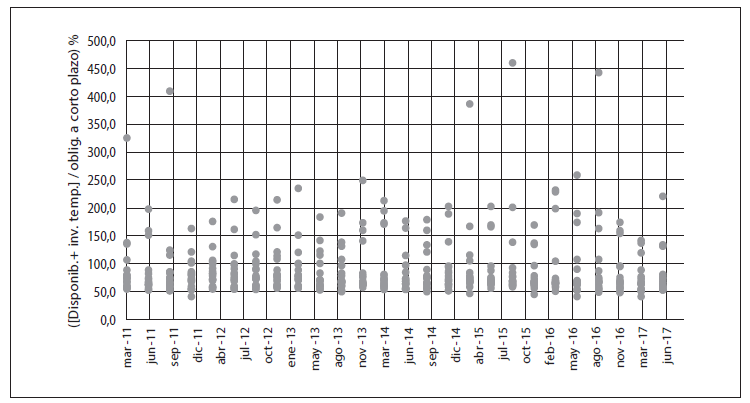
* Evolución: de 5 de marzo a 17 de junio.
Fuente: información de ASFI (Bolivia).
Gráfico 3-B
Variable ([disponibilidades + inversiones temporarias] /
obligaciones a corto plazo) % para las 19 entidades del SBCB*
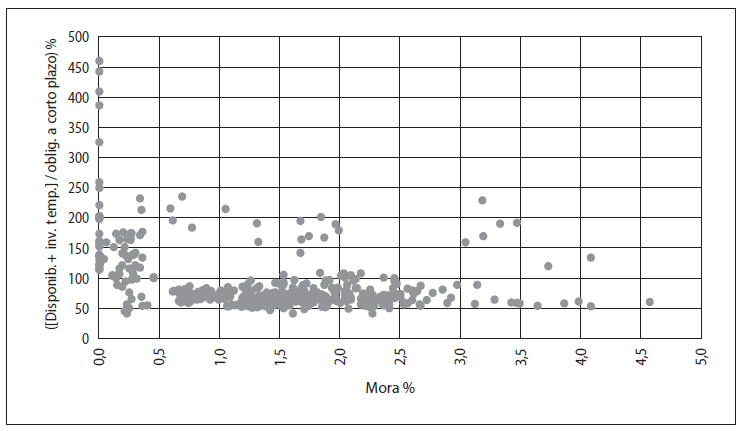
* Dispersión comparativa con la variable Mora %. Evolución: de 5 de marzo a 17 de junio. Fuente: información de ASFI (Bolivia).
El ratio de cobertura de liquidez de corto plazo que incluye las inversiones temporarias cambia de 153 % a finales de 2005 a 246 % a finales de 2009, y se llega a reducir hasta alcanzar un valor de 41 % en junio de 2017.
El último análisis gráfico presentado en esta sección corresponde a la variable económica identificada: el crecimiento interanual del PIB trimestral:
Gráfico 4-A
Variable crecimiento interanual del PIB trimestral*
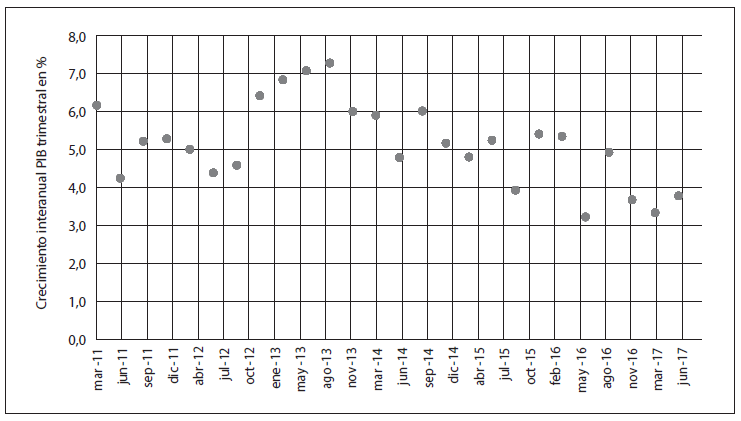
* Evolución: de 5 de marzo a 17 de junio.
Fuente: información de Instituto Nacional de Estadística (Bolivia).
Elaboración propia.
Gráfico 4-B
Variable crecimiento interanual del PIB trimestral, dispersión comparativa
con la variable Mora % para las 19 entidades del SBCB*
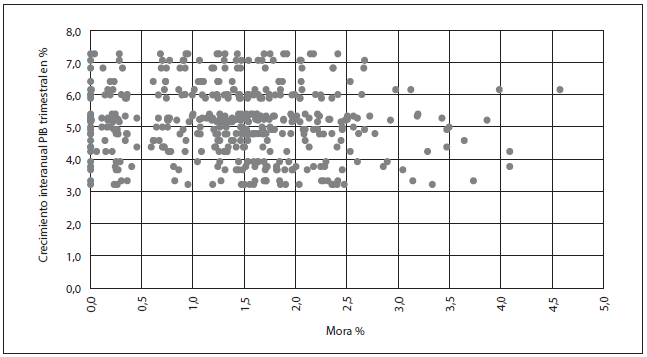
* Evolución: de 5 de marzo a 17 de junio.
Fuente: cálculos a partir de información de Instituto Nacional de Estadística (Bolivia) para crecimiento y Autoridad
de Supervisión del Sistema Financiero (Bolivia) para mora.
Esta variable representa al crecimiento económico y se espera una correlación negativa con el índice de mora la tendencia es ligeramente decreciente.
Matriz de correlaciones
y estadísticos descriptivos
A continuación, se presenta la tabla 4 de correlación entre las variables.
Tabla 4
Correlación variables significativas
| Variables | |||||
|---|---|---|---|---|---|
| y1 | c1 | x1 | x39 | ||
| Variables | Mora % (y1) | 1 | |||
| Crecimiento económico: variación interanual PIB trimestral (c1) | -0,08 | 1 | |||
| Estructura activos: disponibilidades / activos (x1) | 0,09 | 0 | 1 | ||
| Liquidez: (disponib. + inv. temp.) / oblig. a corto plazo (x39) | 0,66 | -0,09 | 0,18 | 1 | |
Elaboración propia.
La matriz de correlaciones (tabla 4) muestra que no existen correlaciones muy cercanas a 1 o -1, por lo tanto, es razonable suponer que no existe una dependencia lineal fuerte entre variables independientes, o entre la variable dependiente y las variables independientes, es decir, no están fuertemente correlacionadas. Estos hechos permiten hipotetizar que, por un lado, podría no existir problemas de multicolinealidad para el modelo (no hay correlaciones altas entre las variables independientes), y por otro lado, que podrían no existir problemas de endogeneidad (no existen correlaciones altas de las variables independientes con la variable dependiente).
A pesar de estos resultados, en la formalización del modelo se trata a la variable c1 (variación interanual del PIB trimestral) como una variable endógena; sustentados en la revisión teórica que, por un lado, indica que la estabilidad financiera causa al crecimiento económico, pero por otro que el crecimiento económico causa estabilidad financiera.
A continuación, en la tabla 5 se presenta un resumen de los principales estadísticos descriptivos de las variables utilizadas en el modelo.
Tabla 5
Estadísticos descriptivos de las variables (dependiente e independientes)
| Variable | Obs. | Media | Desv. est. | Min. | Max. |
|---|---|---|---|---|---|
| Mora % (y1). | 877 | 0,06 | 0,15 | 0,00 | 1,00 |
| Crecimiento económico: variación interanual PIB trimestral (c1). | 877 | 0,05 | 0.01 | 0,02 | 0,07 |
| Estructura activos: disponibilidades / activos (x1). | 877 | 0,15 | 0,12 | 0,01 | 0,91 |
| Liquidez: (disponib. + inv. temp.) / oblig. a corto plazo (x39). | 877 | 1,66 | 5,80 | 0,37 | 91,38 |
Elaboración propia.
Metodología econométrica
El problema planteado en el presente documento requiere la aplicación de un modelo lineal dinámico que permita modelar la probabilidad de incumplimiento y, debido a que el conjunto de información disponible es un panel de datos de bancos (individuos) a través de 12 años con periodicidad trimestral (tiempo), se utiliza la técnica de Arellano-Bond (1991) también conocida como difference GMM (método generalizado de momentos, por sus siglas en inglés) por utilizar como instrumentos las diferencias de los rezagos de la variable dependiente.
Para describir la especificación de este modelo se parte de un modelo lineal estático:
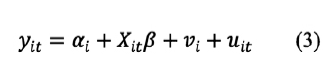
Donde:
Los subíndices i, t denotan al individuo i (banco) para un período determinado
(trimestre).
yit es la variable dependiente observada para el individuo i en el período t; para el caso de este estudio se utiliza la mora como medida del riesgo de crédito.
Xit es la matriz de regresores conocidos (1xk); en el caso de este estudio se utiliza el set de indicadores financieros de la entidad y el set de indicadores externos económicos (crecimiento). Debido a que Xit es una matriz, b es un vector de valores, ait es la constante añadida al modelo con el fin de evitar que el valor y las propiedades estadísticas de los estimadores dependan de la media global de los datos, vi es el efecto individual no observado que no varía en el tiempo y uit es el término de error.
El análisis: al incluir rezagos de la variable dependiente como regresores
en (3) se transforma la especificación del modelo en una especificación dinámica,
tomando en cuenta conceptos como ser el momento y la inercia que
genera el estado de la variable dependiente. El objetivo principal de la transformación
de esta especificación está dirigido al tratamiento de problemas de
endogeneidad, ya que se están incorporando en la estimación a las relaciones
de causalidad que se generan en el interior del modelo.
Considerando el caso de m rezagos se tiene:
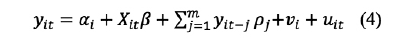
yit-j denota los rezagos de la variable dependiente y pj los parámetros a ser
estimados por cada rezago. Se asume que uit son i.i.d. sobre toda la muestra
con varianza Ϭ2u
; también se asume que vit y uit son independientes para cada
i sobre todos los períodos t; este supuesto es realista, ya que los bancos son
individuos (agentes económicos) independientes entre sí en cuanto a decisiones,
perfil y estrategias, y, por tanto, no actúan bajo influencia de otros, o al
menos no de forma directa.
El caso específico de este estudio es descrito a continuación:
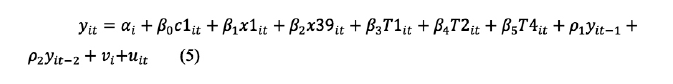
Las variables c1 (crecimiento económico), x1 (ratio disponibilidades sobre activos), x39 (ratio suma de disponibilidades más inversiones temporarias sobre obligaciones a corto plazo), con sus respectivos coeficientes beta (0 al 2) son la desagregación de Xit β de la ecuación genérica (4).
Las suma de las variables yit - 1 (mora rezagada un trimestre) y yit - 2 (mora
rezagada dos trimestres), con sus respectivos coeficientes p1 y r2 y son la
desagregación de la expresión 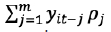 de la ecuación genérica (4).
de la ecuación genérica (4).
Para obtener estimaciones consistentes de los coeficientes de interés se utiliza el estimador difference GMM, en la que se propone estimar la ecuación (5) mediante la aplicación de la primera diferencia, con el fin de eliminar las características específicas no observadas y que no varían en el tiempo vi:
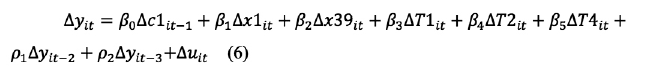
Los rezagos en niveles son utilizados como instrumentos para variables definidas por los autores de la metodología como débilmente exógenas, mientras que las diferencias de las variables son utilizadas como instrumentos de las variables exógenas.
Por construcción, los rezagos de la variable mora son endógenos con la variable mora y, por otro lado, se considera a la variable crecimiento económico también como endógena con base en la evidencia empírica disponible y discutida en la literatura. Este procedimiento es definido como la identificación de un vector Z de instrumentos que permitan construir los momentos 2 (Δ uit Z) y para estimar la ecuación (6) a través de la metodología difference GMM.
Una metodología alternativa es la de system GMM, basado en lo propuesto por Arellano y Bover (1995) y Blundell y Bond (1998), desarrollada con el fin de hacer frente a paneles con pocos períodos, donde la principal diferencia con difference GMM es la incorporación del uso de rezagos de la diferencia de las variables como instrumentos en la ecuación en niveles. Los resultados de la aplicación de la misma son mostrados en la tabla 6 con fines comparativos.
Modelo desarrollado y presentación de resultados
En esta sección se presentan el análisis y los resultados de la aplicación de la metodología propuesta, a base del primer objetivo de la investigación (aplicabilidad), con el fin de cuantificar el riesgo de crédito de SBCB, conforme al segundo objetivo de la investigación (cuantificación).
Se presenta la especificación del modelo desarrollado mediante la metodología de Arellano-Bond:
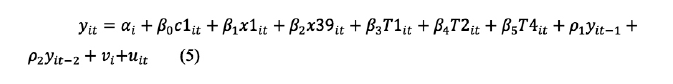
Se utiliza este método para aprovechar la disponibilidad de información, puesto que mediante su uso se trabaja con 877 observaciones para asegurar la mayor cantidad posible de las mismas y conseguir resultados consistentes. Por otro lado, se aplica al modelo la corrección de los errores estándar a base de lo expuesto por Windmeijer (2005).
En la tabla 6 se observan los resultados del modelo final; reporta los resultados de la estimación realizada para la ecuación (1-3), donde, la columna 3 muestra los coeficientes obtenidos mediante la metodología difference GMM, mientras que las columnas 1 y 2 muestran los resultados de estimaciones realizadas bajo el supuesto de que todas las variables explicativas de la ecuación mencionada son estrictamente exógenas. La columna 4 se ha incorporado como una fuente de comparación en base a la metodología seleccionada que es system GMM, conforme a lo expuesto en la sección metodológica; este tipo de modelo ha sido desarrollado para paneles con pocos períodos, ya que la determinación de los estimadores incluye rezagos de diferencias de las variables en la ecuación en niveles. Siendo que este no es el caso, se trabaja principalmente con difference GMM, aunque se muestran los resultados de system GMM de forma comparativa.
El coeficiente de interés analizado en este estudio para la variable crecimiento económico muestra signo negativo en todas las estimaciones. El hallazgo empírico de la relación inversa (a través del signo negativo) entre el crecimiento económico y la mora es relevante y ratifica la lógica esperada de que a mayor crecimiento económico que representa el nivel de ingreso, la mora que es utilizada como la medida del riesgo de crédito se reduce.
Tabla 6
Modelo desarrollado1
| Crecimiento económico tratada como | Exógena | Débilmente exógena | Endógena | |
|---|---|---|---|---|
| Estimador | Pooled | Within + | Arellano- Blundell-Bond (Difference) | Arellano- Blundell-Bond (System) |
| Variables | (1) | (2) | (3) | (4) |
| Mora (t-1) | 0,4624 | 0,5782* | 0,5008* | 0,7266* |
| (0,3498) | (0,0358) | (0,1503) | (0,1336) | |
| Mora (t-2) | -0,0437 | 0,0813* | -0,0295 | 0,1955 |
| (0,1919) | (0,0255) | (0,0645) | (0,1284) | |
| Crecimiento económico: variación interanual PIB trimestral (c1). | -0,2465** | -0,2604* | -0,3508* | -0,2852* |
| (0,1150) | (0,0636) | (0,1033) | (0,0855) | |
| Estructura activos: disponibilidades / activos (x1). | -0,1660 | -0,1762* | -0,1730* | -0,0117* |
| (0,2364) | (0,0183) | (0,0435) | (0,0034) | |
| Liquidez: (disponib. + inv. temp.) / oblig. a corto plazo (x39). | 0,0017*** | 0,0003 | 0,0017* | 0,0021* |
| (0,0010) | (0,0019) | (0,0002) | (0,0003) | |
| Trimestre 1 | -0,0192 | -0,0296** | -0,0037* | -0,0055* |
| (0,0359) | (0,0146) | (0,0008) | (0,0019) | |
| Trimestre 2 | -0,0107 | -0,0169** | -0,0022 | -0,0004 |
| (0,0211) | (0,0082) | (0,0019) | (0,0007) | |
| Trimestre 4 | 0,0060 | 0,0120*** | 0,0003 | 0,0005 |
| (0,0215) | (0,0063) | (0,0006) | (0,0005) | |
| Constante (c) | 0,0595 | 0,0601* | 0,0667* | 0,0160* |
| (0,0600) | (0,0084) | (0,0078) | (0,0049) | |
| Correlación serial (p-value)° | 0,7168 | 0,3783 | ||
| Sargan (p-value)°° | 0,0711 | 1.0000°°° | ||
| Obs. | 824 | 824 | 801 | 824 |
1. La variable dependiente es mora. Se muestran los coeficientes calculados y entre paréntesis se muestran
los errores estándar robustos para el caso de (1) y (2); para el caso de (3) se muestran los errores estándar
robustos Windmeijer; solamente para el caso (4) se muestran errores estándar convencionales GMM debido
a una restricción computacional.
* Indica que la variable es significativa al 1 %.
** Indica que la variable es significativa al 5 %.
*** Indica que la variable es significativa al 10 %.
° Para los modelos difference y system (GMM) la hipótesis nula indica que los errores de la regresión en primera
diferencia no muestran correlación serial de segundo orden.
°° Para los modelos difference y system (GMM) la hipótesis nula indica que los instrumentos no están correlacionados
con los residuos. Calculado con una estimación preliminar del modelo en un paso (one-step), a menos
que se indique lo contrario.
°°° Calculado con el modelo de dos pasos (two step), cabe indicar que de acuerdo a lo establecido por Arellano y
Bond encontraron evidencia de que este test puede subrechazar o desestimar bajo la presencia de heteroscedasticidad.
+ Se ha contrastado mediante el test de Hausman la especificación Within y Between bajo la Ho: Diferencia entre
los coeficientes no es sistemática, la Prob > Chi2 es de 0,00, razón por la cual se utiliza el estimador Within.
La prueba de inexistencia de multicolinealidad es positiva, puesto que los valores VIF son inferiores al valor
de 10 (el valor máximo calculado es de 8,55), permitiendo que no se rechace la hipótesis de la existencia de
multicolinealidad.
Las variables dummy son incluidas como instrumento para controlar cualquier problema estacional (son tres
por la periodicidad trimestral).
Elaboración propia.
Evaluación de especificaciones dinámicas
Se presentan los resultados de los tests de no sobreidentificación y no correlación serial, que son condiciones necesarias, siguiendo la metodología explicada por Abrigo y Love (2015) sobre la base de lo expuesto por Arellano y Bond (1991) para validar la especificación de los modelos dinámicos desarrollados en este estudio.
Test de no sobreidentificación
Este test está destinado a validar el supuesto de que los instrumentos no tienen correlación con los residuos y, por lo tanto, los instrumentos utilizados son válidos en la especificación del modelo. Al usar el método generalizado de momentos como procedimiento para la identificación de los estimadores, se presentan los resultados del test de Sargan:
Table 7
Test de Sargan
| Estadístico/ Prob. | Valor |
|---|---|
| chi2 (673) | 743,18 |
| Prob > chi2 | 0,0711 |
Elaboración propia.
Para la ejecución de este test se realiza la estimación del modelo difference GMM en un paso,1 donde la hipótesis nula es que los instrumentos no tienen una correlación con los residuos. La prob > chi2 del test de Sargan (test de sobreidentificación) es de 0,07, lo que es mayor que 0,05. Esto indica que no se rechaza la hipótesis nula del cumplimiento de las restricciones de sobreidentificación, por tanto, se puede argumentar que los instrumentos utilizados para la estimación son válidos.2
Test de no correlación serial
Este test es aplicado sobre las diferencias de los residuos de la especificación final del modelo, que a diferencia del test anterior es obtenida mediante la metodología difference GMM en dos pasos.
Tabla 8
Test de Arellano-Bond
| Orden | z | Prob>z |
|---|---|---|
| 1 | -1,23 | 0,22 |
| 2 | 0,36 | 0,72 |
Elaboración propia.
En el caso de este test, la hipótesis nula indica que los errores de la regresión en primera diferencia no muestran correlación serial de segundo orden; se tiene como resultado la probabilidad P > z de los residuos de orden 2 tienen un valor de 0,72, lo que es superior al valor de 0,05. Esto permite que no se rechace la hipótesis nula.3
Cuantificación del riesgo de crédito
A continuación, se cuantifica el riesgo de crédito basado en la estimación de la variable dependiente con el modelo desarrollado:
Normalización de la variable
Sobre la base del modelo desarrollado se puede obtener la probabilidad
de incumplimiento ajustada del modelo o esperada para cada entidad y para
cada trimestre de la muestra analizada, a partir de la función lineal.
Debido a que los valores ajustados del modelo podrían estar fuera del
rango 0 a 1 necesario para la probabilidad de incumplimiento, se aplica la
función de normalización característica de escala del tipo:
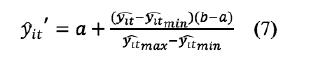
Donde:
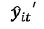 denota el valor estimado de mora mediante la especificación de Arellano
y Bond y normalizado; por lo tanto, es la mora estimada en su estado
natural;
denota el valor estimado de mora mediante la especificación de Arellano
y Bond y normalizado; por lo tanto, es la mora estimada en su estado
natural; 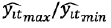 denotan el valor máximo y valor mínimo que asume la
mora estimada, ‘a’ es el valor mínimo del rango de la escala a la que se quiere
ajustar para la mora estimada, y ‘b’ es el valor máximo del rango de la escala
a la que se quiere ajustar para la mora estimada.
denotan el valor máximo y valor mínimo que asume la
mora estimada, ‘a’ es el valor mínimo del rango de la escala a la que se quiere
ajustar para la mora estimada, y ‘b’ es el valor máximo del rango de la escala
a la que se quiere ajustar para la mora estimada.
Dado que la escala deseada está entre a = 0 y b = 1 se puede expresar
(1-5) de la siguiente forma:
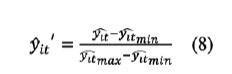
A continuación, se presenta en el gráfico 5 la normalización de la variable
probabilidad de incumplimiento 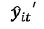 ; esta normalización es realizada en
la escala 0 a 1 y se denota como
; esta normalización es realizada en
la escala 0 a 1 y se denota como 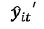
Gráfico 5
Normalización de la variable mora estimada (y1) en la escala 0 a 1
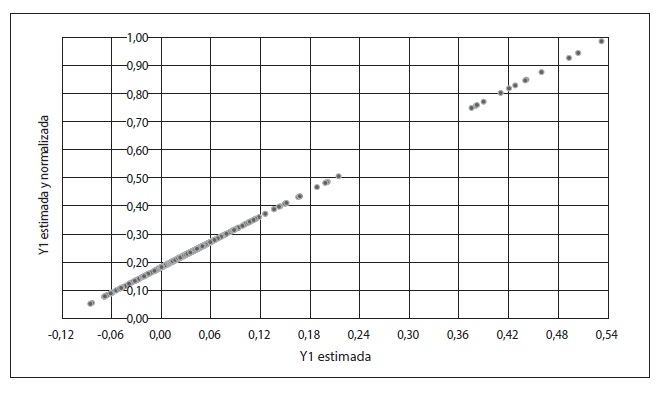
Elaboración propia.
Como se puede observar en el gráfico 5, la transformación es lineal manteniendo las distancias entre cada observación de forma proporcional a la nueva escala de la variable probabilidad de incumplimiento.
En los gráficos 6-A y 6-B se puede observar la transformación que mantiene las mismas características de distancia entre las proporciones a lo largo del período analizado; la única diferencia es la escala que en la variable estimada original está entre -0,12 y 0,54, mientras que al ser normalizada es llevada a la escala 0 a 1.
Gráfico 6-A
Normalización de la variable mora estimada (y1) escala inicial
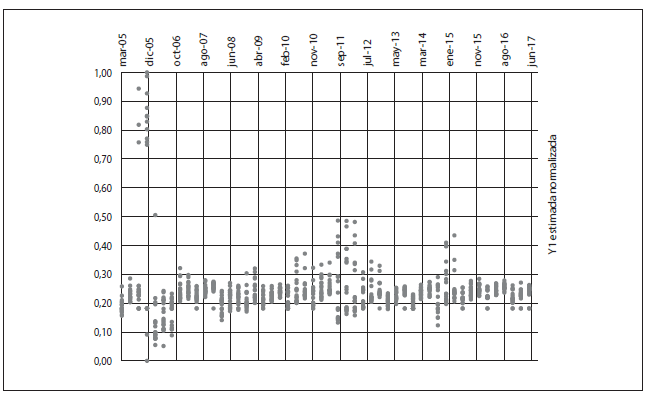
Elaboración propia.
Gráfico 6-B
Normalización de la variable mora estimada (y1) ajustada en la escala 0 a 1
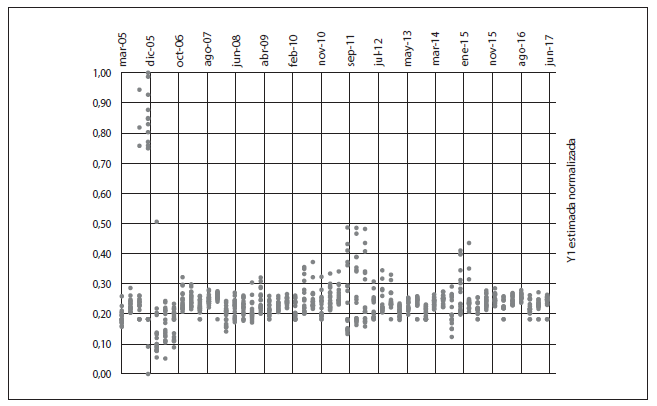
Elaboración propia.
Aplicación de la probabilidad de incumplimiento a la cartera con incumplimiento
Se presenta el cálculo de la probabilidad de incumplimiento del sistema financiero consolidado en el período de análisis (de marzo 2005 a junio 2017).
La probabilidad de incumplimiento esperada debe ser ajustada por la cartera con incumplimiento, que para fines de este estudio es definida como la cartera con calificación diferente de A.4
Adicionalmente se presenta una aproximación de la probabilidad de incumplimiento agregada (PD), aplicada efectivamente a la cartera del SBCB.
Tabla 9
Probabilidad de incumplimiento calculada
| Mes | Pérdida esperada constituida mm USD | Pérdida esperada calculada mm USD | Total cartera mm USD | % Pérdida esperada constituida / total cartera | % Pérdida esperada calculada / total cartera |
|---|---|---|---|---|---|
| dic-05 | 239 | 224 | 3,328 | 7,2 | 6,7 |
| dic-06 | 220 | 163 | 3,593 | 6,1 | 4,5 |
| dic-07 | 196 | 158 | 4,277 | 4,6 | 3,7 |
| dic-08 | 227 | 150 | 5,109 | 4,4 | 2,9 |
| dic-09 | 198 | 144 | 5,745 | 3,4 | 2,5 |
| dic-10 | 168 | 118 | 6,916 | 2,4 | 1,7 |
| dic-11 | 169 | 166 | 8,798 | 1,9 | 1,9 |
| dic-12 | 176 | 166 | 10,649 | 1,7 | 1,6 |
| dic-13 | 199 | 166 | 12,981 | 1,5 | 1,3 |
| dic-14 | 233 | 233 | 15,186 | 1,5 | 1,5 |
| dic-15 | 268 | 272 | 18,178 | 1,5 | 1,5 |
| dic-16 | 302 | 252 | 21,211 | 1,4 | 1,2 |
| dic-17 | 329 | 306 | 21,996 | 1,5 | 1,4 |
Elaboración propia.
Gráfico
SBCB: probabilidad de incumplimiento calculada y constitución real
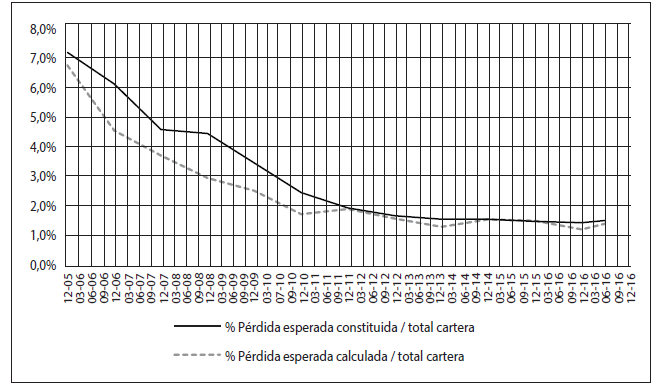
Elaboración propia.
Como se observa en la tabla 9 y el gráfico 7, al comparar la probabilidad de incumplimiento del sistema analizado (representada como la tasa entre la pérdida esperada calculada y la cartera del sistema), se puede observar que los valores obtenidos plantean un menor nivel de previsión requerido de forma consistente durante el período de análisis, en comparación a la previsión efectiva realizada con excepción del año 2015, que se calcula de un requerimiento levemente superior al constituido.
De acuerdo con estos resultados, el nivel de previsión establecido por el ente regulador es suficiente, e incluso muestra una sobreprevisión para la coyuntura financiera y económica del año 2017, y también durante el período analizado. Otro aspecto interesante es que la brecha entre el valor constituido y el calculado se ha ido reduciendo.
Con base en los resultados obtenidos, se ha demostrado la aplicabilidad de una metodología adaptada al cálculo de la pérdida esperada; por otro lado, se ha determinado que la medida de pérdida esperada del sistema bancario comercial boliviano es adecuada para el nivel de riesgo de crédito existente. Estas conclusiones se constituyen en el aporte de esta investigación.
Conclusiones
En este artículo se han presentado temas relacionados a la cuantificación del riesgo de crédito de forma agregada en sistemas bancarios, debido a la necesidad (y oportunidad) identificada sobre la aplicación de este tipo de mediciones a nivel macro o agregado, aprovechando la disponibilidad de tecnología que se utiliza en el campo de las finanzas a nivel micro o empresarial. Otra oportunidad identificada ha sido la condición del mercado financiero boliviano, en el que predomina el mercado bancario comercial, característica que ha desaparecido (o nunca ha existido) en economías avanzadas que a su vez son productoras del material científico económico y financiero y en las cuales no se puede aislar el impacto de la banca de inversión por la alta interrelación que tiene con todos los sectores.
Se ha presentado la adaptación de una metodología utilizada típicamente a nivel micro por los bancos para el cálculo de la pérdida esperada de los clientes; esta adaptación ha combinado de forma innovadora el concepto del Credit Scoring (para asignar a la cartera una probabilidad de incumplimiento), pero a través de una técnica econométrica más avanzada, basada en paneles dinámicos seleccionando estimadores, que permiten controlar la presencia de endogeneidad bajo los supuestos planteados en el documento y además explotando la información de incumplimiento de forma lineal y no así binaria.
El resultado obtenido en la aplicación muestra que la previsión por cartera incobrable actual en el SBCB es superior a la determinada por el modelo basado en el indicador de probabilidad de incumplimiento (PD), ya que para junio de 2017 el valor esperado es de 1,4 % de la cartera total, mientras que el constituido es de 1,5 %.
Esta aplicación es útil tanto para tomadores de decisiones privados (los bancos) como para reguladores y administradores de política económica, ya que con la cuantificación del riesgo de crédito se puede planificar la cobertura de acciones de política económica necesarias para mantener el sistema bancario sano y de este modo asegurar la fortaleza del sistema económico.
Notas
1 El modelo auxiliar no es utilizado para la predicción de los resultados de este estudio.
2 El modelo system GMM, presentado en la tabla 6 con fines comparativos, no cumple con esta condición al ejecutar el procedimiento en un paso; sin embargo, al ejecutar la especificación en dos pasos el p-value es mayor a 5 %, cabe indicar que de acuerdo a lo establecido por Arellano y Bond (1991) encontraron evidencia de que este test puede subrechazar o desestimar bajol a presencia de heteroscedasticidad.
3 En el caso de la especificación de system GMM, el p-value es de 0,38, por lo que tampoco se rechaza la hipótesis nula.
4 En Bolivia se aplica la calificación de la cartera de créditos de forma estándar de acuerdo a lo establecido por el ente regulador; el rango de calificación va desde A hasta F, donde la calificación A es la cartera de mejor calidad y la calificación F es la cartera de peor calidad.
Referencias
Abrigo, Michael Ralph, e Inessa Love. 2016. “Estimation of Panel Vector Autoregression in Stata: A package of Programs”. Manoa: University of Hawaii at Manoa. https://bit. ly/33DDqnJ.
Acemoglu, Daron, Simon Johnson y James A. Robinson. 2005. “Los orígenes coloniales del desarrollo comparativo: una investigación empírica”. Revista de Economía Institucional 7 (13): 17-67. https://bit.ly/3c6EGne.
Arellano, Manuel, y Stephen Bond. 1991. “Some Tests of Specification for Panel Data: Monte Carlo Evidence and an Application to Employment Equations”. Review of Economic Studies 58 (2): 277-297. https://bit.ly/3hEj2rp.
Arellano, Manuel, y Olympia Bover. 1995. “Another Look at the Instrumental Variable Estimation of Error-components Models”. Journal of Econometrics 68 (1): 29-51. https://bit. ly/2Ec4X6Z.
Aver, Bostjan. 2008. “An empirical Analysis of Credit Risk Factors of the Slovenian Banking System”. Managing Global Transitions 6 (3): 317-334. https://bit.ly/2RCybz4.
Ayyagari, Meghana, Thorsten Beck y María Martínez-Peria. 2017. “Credit Growth and Macroprudential Policies: Preliminary Evidence on the Firm Level”. Basilea: BIS Papers. https://bit.ly/3hLE1sl.
Basel Committee on Banking Supervision. 2017. “Basel III: Finalising Post-crisis Reforms”. Bank for International Settlements. Basilea: https://bit.ly/2FI2uSD.
Başkaya, Yusuf, Julian di Giovanni, Sebnem Kalemli-Özcan, Jose-Luis Peydro y Mehmet Ulu. 2016. “Capital Flows, Credit Cycles and Macroprudential Policy”. Basilea: BIS Papers. https://bit.ly/35Hkc3g.
Bellotti, Anthony, y Jonathan Crook. 2009. “Credit Scoring with Macroeconomic Variables Using Survival Analysis”. Journal of the Operational Research Society 60 (12): 1699- 1707. https://bit.ly/33F2iLH.
Berger, Allen, y Robert De Young. 1997. “Problem Loans and Cost efficiency in Commercial Banks”. Journal of Banking and Finance 21 (6): 849-870. https://bit.ly/2Fxcka1.
Blundell, Richard, y Stephen Bond. 1998. “Initial Conditions and Moment Restrictions in Dynamic Panel Data Models”. Journal of Econometrics 87: 115-143. https://bit.ly/3iNndms.
Bohachova, Olga. 2008. “The Impact of Macroeconomic Factors on Risks in the Banking Sector: A Cross-country Empirical Assessment”. IAW Discussion Papers 44. Tubinga: https:// bit.ly/3c7Kgpv.
Chen, Hsin-Hung, Ben-Chang Shia y Hsiu-Yu Lee. 2011. “A Comparative Analysis of Credit Risk Management Models for Banking Industry Using Simulation”. Applied Economics, Business and Development 208: 554-562. https://bit.ly/2F65GH6.
Choi, Woon Gyu. 2017. “Comments on “Household Credit in Asia-Pacific”. Basilea: BIS Papers. https://bit.ly/3ksUV0W.
Crook, Jonathan, David Edelman y Lyn Thomas. 2007. “Recent Developments in Consumer Credit Risk Assessment”. European Journal of Operational Research 183: 1447-1465. https://bit.ly/3mwbOtl.
Deng, Yongheng. 2017 “Comments on Household Credit, Growth and Inequality in Malaysia: Does the Type of Credit Matter?”. Basilea: BIS Papers. https://bit.ly/2Fxd92B.
Dionne, Georges. 2013. “Risk Management: History, Definition and Critique”. CIRRELT- 2013-7. Interuniversity Research Centre on Enterprise Networks. Québec: Logistic and Transportation. https://bit.ly/32Ga1Kf.
De Guimarães e Souza, Gustavo, y Carmem Feijó. 2011. “Credit Risk and Macroeconomic Interactions: Empirical Evidence from the Brazilian Banking System”. Modern Economy 2 (5): 910-929. https://bit.ly/3cdkmRg.
Esfahani, Salehi, y María Ramírez. 2003. “Institutions, Infrastructure, and Economic Growth”. Journal of Development Economics 70 (2): 443-477. https://bit.ly/3lQFYHp.
Fendoğlu, Salih. 2016. “Credit Cycles and Macroprudential Policy Framework in Emerging Countries”. Basilea: BIS Papers, Macroprudential Policy 86. https://bit.ly/2FwdGBS.
Finlay, Steven. 2009. “Credit Scoring for Profitability Objectives”. European Journal of Operational Research 202: 528-537. https://bit.ly/3hCxOip.
Greene, William. 1998. “Sample Selection in Credit Scoring Models”. Japan and the World Economy 10 (3): 317-320. https://bit.ly/2FRZDpG.
Gurný, Petr, y Martin Gurný. 2013. “Comparison of Credit Scoring Models on Probability of Default Estimation for US banks”. Prague Economic Papers 22: 163-181. https://bit. ly/2Ec8W3r.
Heckman, James. 1979. “Sample Selection Bias as a Specification Error”. Econometrica 47 (1): 156-162. https://bit.ly/2ZIz7X9.
Hoggarth, Glenn. 2017. “Comments on ‘Foreign Banks and Credit Conditions in EMES’ ”. Basilea: BIS Papers. https://bit.ly/3kwJmWz.
Jakubík, Petr. 2007. “Macroeconomic Environment and Credit Risk”. Czech Journal of Economics and Finance 57 (1-2): 60-78. https://bit.ly/35IFddT.
Kattai, Rasmus. 2010. “Credit Risk Model for the Estonian Banking Sector”. Tallin: Bank of Estonia. https://bit.ly/35O79gC.
Lessman, Stefan, Bart Baesens, Hain-Vonn Seow y Lyn Thomas. 2015. “Benchmarking State- of-the-art Classification Algorithms for Credit Scoring: An Update of Research”. European Journal of Operational Research 247 (1): 124-136. https://bit.ly/2ZIAyF1.
McGuire, Patrick, y Torsten Ehlers. 2017. “Foreign Banks and Credit Conditions in EMES”. Basilea: BIS Papers. https://bit.ly/2RBbtHJ.
Nkusu, Mwanza. 2011. “Nonperforming Loans and Macrofinancial Vulnerabilities in Advanced Economies”. Washington D. C: FMI. https://bit.ly/35KLy8u.
Pak-Wing, Tom, y Chun-shan Wong. 2008. “Stress Testing Banks’ Credit Risk Using Mixture Vector Autoregressive Models”. Hong Kong: Hong Kong Monetary Authority. https://bit. ly/2ZNd69o.
Park, Jaeh-Ha. 2017. “Comments on Credit Growth and Macroprudential Policies: Preliminary Evidence on the Firm Level”. Basilea: BIS Papers. https://bit.ly/3iHmy5D.
Ravalo, Johnny. 2017. “Credit Build-up and Financial Stability Issues: Do We Know Enough to Calibrate Appropriate Intervention?”. Basilea: BIS Papers. https://bit.ly/3iHUK1c.
Rocha, María, Joao Gama y Elísio Brandao. 2013. “Introducing Time-changing Economics Into Credit Scoring”. https://bit.ly/2RC7n1R.
Salas, Vicente, y Jesús Saurina. 2002. “Credit Risk in Two Institutional Regimes: Spanish Commercial and Saving Banks”. Journal of Financial Services Research 22 (3): 203-224. https://bit.ly/3kvtiV4.
Santos, Tano. 2015. “Credit Booms: Implications for the Public and the Private Sector”. Basilea: BIS Papers. https://bit.ly/2Hd272P.
Schularick, Moritz, e Ilhyock Shim. 2017. “Household Credit in Asia-Pacific”. Basilea: BIS Papers. https://bit.ly/2RDfpru.
Soh, Jiaming, Amanda Chong y Kue-Peng Chuah. 2017. “Household Credit, Growth and Inequality in Malaysia: Does the Type of Credit Matter?”. Basilea: BIS Papers. https:// bit.ly/3ktySHc.
Tomas, Lyn. 2010. “Consumer Finance: Challenges for Operational Research”. Journal of the Operational Research Society 61: 41-52. https://bit.ly/2ZNGPzo.
Torrico, Sergio. 2014. “Macro Credit Scoring como propuesta para cuantificar el riesgo de crédito”. Investigación & Desarrollo 15 (2): 42-63. https://bit.ly/2ZNFbxH.
Wickens, Michael. 2011. “A DSGE Model of Banks and Financial Intermediation with Default risk”. CEPR: Londres. https://bit.ly/2RyWSfQ.
Windmeijer, Frank. 2005. “A Finite Sample Correction for the Variance of Linear Efficient Two-step GMM Estimators”. Journal of Econometrics 126: 25-51. https://bit.ly/2ZQI3d8.